diff --git a/.travis.yml b/.travis.yml
index 33fab68..96fca8d 100644
--- a/.travis.yml
+++ b/.travis.yml
@@ -1,24 +1,15 @@
language: julia
julia:
- - 1.0
- 1
os:
- linux
- osx
+ - windows
-notifications:
- email:
- - sunbergzach@gmail.com
-
-# after_success:
-# - julia --project -e 'import Pkg; Pkg.add("Documenter"); include("docs/make.jl")'
-# - julia --project -e 'import Pkg; Pkg.add("Coverage"); using Coverage; Codecov.submit(Codecov.process_folder())'
-script:
- - git clone https://github.com/JuliaRegistries/General $(julia -e 'import Pkg; println(joinpath(Pkg.depots1(), "registries", "General"))')
- - git clone https://github.com/JuliaPOMDP/Registry $(julia -e 'import Pkg; println(joinpath(Pkg.depots1(), "registries", "JuliaPOMDP"))')
- - if [[ -a .git/shallow ]]; then git fetch --unshallow; fi
- - julia --project --color=yes --check-bounds=yes -e 'import Pkg; Pkg.build(); Pkg.test("POMDPExamples"; coverage=true)'
+# script:
+# - if [[ -a .git/shallow ]]; then git fetch --unshallow; fi
+# - julia --project --color=yes --check-bounds=yes -e 'import Pkg; Pkg.build(); Pkg.test("POMDPExamples"; coverage=true)'
after_success:
- julia --project --color=yes -e 'import Pkg; Pkg.add("Coverage"); using Coverage; Codecov.submit(Codecov.process_folder())'
diff --git a/Project.toml b/Project.toml
index 2e5cccd..26b4266 100644
--- a/Project.toml
+++ b/Project.toml
@@ -6,7 +6,10 @@ version = "0.2.0"
[deps]
BasicPOMCP = "d721219e-3fc6-5570-a8ef-e5402f47c49e"
BeliefUpdaters = "8bb6e9a1-7d73-552c-a44a-e5dc5634aac4"
+D3Trees = "e3df1716-f71e-5df9-9e2d-98e193103c45"
+DiscreteValueIteration = "4b033969-44f6-5439-a48b-c11fa3648068"
FIB = "13b007ba-0ca8-5af2-9adf-bc6a6301e25a"
+MCTS = "e12ccd36-dcad-5f33-8774-9175229e7b33"
POMDPModelTools = "08074719-1b2a-587c-a292-00f91cc44415"
POMDPModels = "355abbd5-f08e-5560-ac9e-8b5f2592a0ca"
POMDPPolicies = "182e52fb-cfd0-5e46-8c26-fd0667c990f4"
@@ -17,7 +20,7 @@ Printf = "de0858da-6303-5e67-8744-51eddeeeb8d7"
Random = "9a3f8284-a2c9-5f02-9a11-845980a1fd5c"
[compat]
-POMDPs = "0.8"
+POMDPs = "0.9"
julia = "1"
[extras]
diff --git a/README.md b/README.md
index b7a686f..d9d2be6 100644
--- a/README.md
+++ b/README.md
@@ -15,12 +15,12 @@ Each tutorial is a notebook in the notebooks directory. Here is a list:
- [Using an Offline Solver](notebooks/Using-an-Offline-Solver.ipynb)
- [Using an Online Solver](notebooks/Using-an-Online-Solver.ipynb)
- [Defining a Heuristic Policy](notebooks/Defining-a-Heuristic-Policy.ipynb)
+- [Defining MDP of gridWorld and using VI and MCTS to find solutions](notebooks/GridWorld.ipynb)
## Legacy tutorials
There are also several tutorials contained in the [legacy folder](legacy) which are not tested and may not be up to date, but may nevertheless be useful.
-- [GridWorld](legacy/GridWorld.ipynb)
- [Tiger](legacy/Tiger.ipynb)
- [RL](legacy/rl-tuto/reinforcement_learning_tutorial.ipynb)
diff --git a/legacy/GridWorld.ipynb b/legacy/GridWorld.ipynb
deleted file mode 100644
index 9f6578d..0000000
--- a/legacy/GridWorld.ipynb
+++ /dev/null
@@ -1,1560 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "# Grid World Tutorial: POMDPs.jl for Complete Beginners"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "In this tutorial, we try to provide a simple example of how to define a Markov decision process (MDP) problem using the [POMDPs.jl](https://github.com/sisl/POMDPs.jl) interface. After defining the problem in this way, you will be able to use the solvers that the interface supports. In this tutorial, we will show you how to use the value iteration and the Monte Carlo Tree Search solvers that the POMDPs.jl interface supports. We assume that you have some knowledge of basic programming, but are not necessarily familiar with all the features that exist in Julia. We try to cover the many language specific features used in POMDPs.jl in this tutorial. We do assume that you know the grid world problem, and are familiar with the formal defintion of the MDP. Let's get started!"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Dependencies\n",
- "You need to install a few modules in order to use this notebook. If you have all the modules below installed, great! If not run the following commands:\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "collapsed": false
- },
- "source": [
- "```julia\n",
- "# install the POMDPs.jl interface\n",
- "Pkg.add(\"POMDPs\")\n",
- "Pkg.add(\"POMDPToolbox\")\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "If you already have all of the modules above, make sure you have the most recent versions. Many of these are still under heavy development, so update before starting by running\n",
- "\n",
- "```julia\n",
- "Pkg.update()\n",
- "```"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "metadata": {
- "collapsed": false,
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "outputs": [],
- "source": [
- "# first import the POMDPs.jl interface\n",
- "using POMDPs\n",
- "\n",
- "# POMDPToolbox has some glue code to help us use Distributions.jl\n",
- "using POMDPToolbox"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Problem Overview\n",
- "In Grid World, we are trying to control an agent who has trouble moving in the desired direction. In our problem, we have a four reward states on a $10\\times 10$ grid. Each position on the grid represents a state, and the positive reward states are terminal (the agent stops recieveing reward after reaching them). The agent has four actions to choose from: up, down, left, right. The agent moves in the desired direction with a probability of 0.7, and with a probability of 0.1 in each of the remaining three directions. The problem has the following form:\n",
- "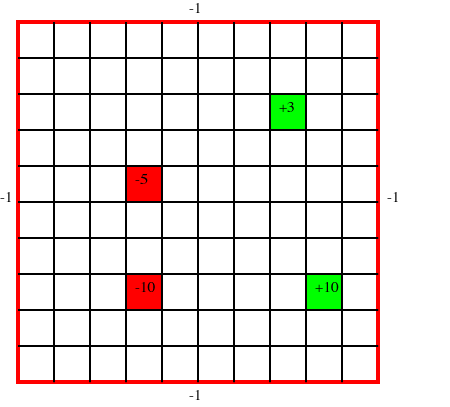"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## MDP Type\n",
- "\n",
- "In POMDPs.jl, an MDP is defined by creating a subtype of the `MDP` abstract type. The types of the states and actions for the MDP are declared as [parameters](https://docs.julialang.org/en/stable/manual/types/#Parametric-Types-1) of the `MDP` type. For example, if our states and actions are both represented by integers we can define our MDP type in the following way:\n",
- "```julia\n",
- "type MyMDP <: MDP{Int64, Int64} # MDP{StateType, ActionType}\n",
- "\n",
- "end\n",
- "```\n",
- "`MyMDP` is a subtype from an abstract MDP type defined in POMDPs.jl. Let's first define types to represent grid worls states and actions, and then we'll go through defining our Grid World MDP type. "
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "slideshow": {
- "slide_type": "slide"
- }
- },
- "source": [
- "## States\n",
- "The data container below represents the state of the agent in the grid world."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "struct GridWorldState \n",
- " x::Int64 # x position\n",
- " y::Int64 # y position\n",
- " done::Bool # are we in a terminal state?\n",
- "end"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Below are some convenience functions for working with the GridWorldState. "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "posequal (generic function with 1 method)"
- ]
- },
- "execution_count": 3,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "# initial state constructor\n",
- "GridWorldState(x::Int64, y::Int64) = GridWorldState(x,y,false)\n",
- "# checks if the position of two states are the same\n",
- "posequal(s1::GridWorldState, s2::GridWorldState) = s1.x == s2.x && s1.y == s2.y"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Actions\n",
- "Since our action is simply the direction the agent chooses to go (i.e. up, down, left, right), we can use a Symbol to represent it. Symbols are essentially the same as strings, but they typically consist of only one word and literals begin with \"`:`\". See [this page](https://stackoverflow.com/questions/23480722/what-is-a-symbol-in-julia) for a techincal discussion of what they are. Note that in this case, we will not define a custom type for our action, instead we represent it directly with a symbol. So that our action looks like:\n",
- "```julia\n",
- "action = :up # can also be :down, :left, :right\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## MDP\n",
- "The GridWorld data container is defined below. It holds all the information we need to define the MDP tuple $$(\\mathcal{S}, \\mathcal{A}, T, R).$$"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 4,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "# the grid world mdp type\n",
- "type GridWorld <: MDP{GridWorldState, Symbol} # Note that our MDP is parametarized by the state and the action\n",
- " size_x::Int64 # x size of the grid\n",
- " size_y::Int64 # y size of the grid\n",
- " reward_states::Vector{GridWorldState} # the states in which agent recieves reward\n",
- " reward_values::Vector{Float64} # reward values for those states\n",
- " tprob::Float64 # probability of transitioning to the desired state\n",
- " discount_factor::Float64 # disocunt factor\n",
- "end"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Before moving on, I want to create a constructor for GridWorld for convenience. Currently, if I want to create an instance of GridWorld, I have to pass in all of fields inside the GridWorld container (size_x, size_y, etc). The function below will return a GridWorld type with all the fields filled with some default values."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 5,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "4-element Array{GridWorldState,1}:\n",
- " GridWorldState(4, 3, false)\n",
- " GridWorldState(4, 6, false)\n",
- " GridWorldState(9, 3, false)\n",
- " GridWorldState(8, 8, false)"
- ]
- },
- "execution_count": 5,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "# we use key worded arguments so we can change any of the values we pass in \n",
- "function GridWorld(;sx::Int64=10, # size_x\n",
- " sy::Int64=10, # size_y\n",
- " rs::Vector{GridWorldState}=[GridWorldState(4,3), GridWorldState(4,6), GridWorldState(9,3), GridWorldState(8,8)], # reward states\n",
- " rv::Vector{Float64}=rv = [-10.,-5,10,3], # reward values\n",
- " tp::Float64=0.7, # tprob\n",
- " discount_factor::Float64=0.9)\n",
- " return GridWorld(sx, sy, rs, rv, tp, discount_factor)\n",
- "end\n",
- "\n",
- "# we can now create a GridWorld mdp instance like this:\n",
- "mdp = GridWorld()\n",
- "mdp.reward_states # mdp contains all the defualt values from the constructor"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Spaces\n",
- "Let's look at how we can define the state and action spaces for our problem."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### State Space\n",
- "The state space in an MDP represents all the states in the problem. There are two primary functionalities that we want our spaces to support. We want to be able to iterate over the state space (for Value Iteration for example), and sometimes we want to be able to sample form the state space (used in some POMDP solvers). In this notebook, we will only look at iterable state spaces. "
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Since we can iterate over elements of an array, and our problem is small, we can store all of our states in an array. If your problem is very large (tens of millions of states), it might be worthwhile to create a custom type to define the problem's state space. See [this](http://stackoverflow.com/questions/25028539/how-to-implement-an-iterator-in-julia) post on stackoverflow on making simple iterators. "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 6,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "function POMDPs.states(mdp::GridWorld)\n",
- " s = GridWorldState[] # initialize an array of GridWorldStates\n",
- " # loop over all our states, remeber there are two binary variables:\n",
- " # done (d)\n",
- " for d = 0:1, y = 1:mdp.size_y, x = 1:mdp.size_x\n",
- " push!(s, GridWorldState(x,y,d))\n",
- " end\n",
- " return s\n",
- "end;"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Here, the code: ```function POMDPs.states(mdp::GridWorld)``` means that we want to take the function called ```states(...)``` from the POMDPs.jl module and add another method to it. The ```states(...)``` function in POMDPs.jl doesn't know about our GridWorld type. However, now when ```states(...)``` is called with GridWorld it will dispatch the function we defined above! This is the awesome thing about multiple-dispatch, and one of the features that should make working with MDP/POMDPs easier in Julia. \n",
- "\n",
- "The solvers that support the POMDPs.jl interface know that a function called ```states(...)``` exists in the interface. However, they do not know the behavior of that function for GridWorld. That means in order for the solvers to use this behavior all we have to do is pass an instance of our GridWorld type into the solver. When ```states(...)``` is called in the solver with the GridWorld type, the function above will be called. "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 7,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- "GridWorldState(1, 1, false)"
- ]
- },
- "execution_count": 7,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "mdp = GridWorld()\n",
- "state_space = states(mdp);\n",
- "state_space[1]"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### Action Space"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "The action space is the set of all actions availiable to the agent. In the grid world problem the action space consists of up, down, left, and right. We can define the action space by implementing a new method of the `actions` function."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 8,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "POMDPs.actions(mdp::GridWorld) = [:up, :down, :left, :right];"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Now that we've defined our state and action spaces, we are half-way thorugh our MDP tuple:\n",
- "$$\n",
- "(\\mathcal{S}, \\mathcal{A}, T, R)\n",
- "$$"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Distributions"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Since MDPs are probabilistic models, we have to deal with probability distributions. In this section, we outline how to define probability distriubtions, and what tools are availiable to help you with the task."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### Transition Distribution "
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "If you are familiar with MDPs, you know that the transition function $T(s' \\mid s, a)$ captures the dynamics of the system. Specifically, $T(s' \\mid s, a)$ is a real value that defines the probabiltiy of transitioning to state $s'$ given that you took action $a$ in state $s$. The transition distirubtion $T(\\cdot \\mid s, a)$ is a slightly different construct. This is the actual distribution over the states that our agent can reach given that its in state $s$ and took action $a$. In other words this is the distribution over $s'$. \n",
- "\n",
- "For this grid world example there are only a few states that the agent can transition to, so there are only a few states that have nonzero probability in $T(\\cdot \\mid s, a)$. Thus, we will use the sparse [categorical distribution](https://en.wikipedia.org/wiki/Categorical_distribution) (`SparseCat`) from POMDPToolbox. [Distributions.jl](https://github.com/JuliaStats/Distributions.jl) also contains some distributions, but in many cases, a custom distribution type will need to be defined - see [the source code for `SparseCat`](https://github.com/JuliaPOMDP/POMDPToolbox.jl/blob/master/src/distributions/sparse_cat.jl) for an example.\n",
- "\n",
- "A `SparseCat` object contains a vector of states and an associated vector of their probabilities. The probabilities of all other states are implied to be zero."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Transition Model"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "In this section we will define the system dynamics of the gird world MDP. In POMDPs.jl, we work with transition distirbution functions $T(s' \\mid s, a)$, so we want to write a function that can generate the transition distributions over $s'$ for us given an $(s, a)$ pair. "
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "In grid world, the dynamics of the system are fairly simple. We move in the specified direction with some pre-defined probability. This is the `tprob` parameter in our GridWorld MDP (it is set to 0.7 in the DMU book example). If we get to state with a positive reward, we've reached a terminal state and can no longer accumulate reward."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "In the transition function we want to fill the neighbors in our distribution d with the reachable states from the state, action pair. We want to fill the probs in our distirbution d with the probabilities of reaching that neighbor. "
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 9,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "# transition helpers\n",
- "function inbounds(mdp::GridWorld,x::Int64,y::Int64)\n",
- " if 1 <= x <= mdp.size_x && 1 <= y <= mdp.size_y\n",
- " return true\n",
- " else\n",
- " return false\n",
- " end\n",
- "end\n",
- "\n",
- "inbounds(mdp::GridWorld, state::GridWorldState) = inbounds(mdp, state.x, state.y);"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 10,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "function POMDPs.transition(mdp::GridWorld, state::GridWorldState, action::Symbol)\n",
- " a = action\n",
- " x = state.x\n",
- " y = state.y\n",
- " \n",
- " if state.done\n",
- " return SparseCat([GridWorldState(x, y, true)], [1.0])\n",
- " elseif state in mdp.reward_states\n",
- " return SparseCat([GridWorldState(x, y, true)], [1.0])\n",
- " end\n",
- "\n",
- " neighbors = [\n",
- " GridWorldState(x+1, y, false), # right\n",
- " GridWorldState(x-1, y, false), # left\n",
- " GridWorldState(x, y-1, false), # down\n",
- " GridWorldState(x, y+1, false), # up\n",
- " ] # See Performance Note below\n",
- " \n",
- " targets = Dict(:right=>1, :left=>2, :down=>3, :up=>4) # See Performance Note below\n",
- " target = targets[a]\n",
- " \n",
- " probability = fill(0.0, 4)\n",
- "\n",
- " if !inbounds(mdp, neighbors[target])\n",
- " # If would transition out of bounds, stay in\n",
- " # same cell with probability 1\n",
- " return SparseCat([GridWorldState(x, y)], [1.0])\n",
- " else\n",
- " probability[target] = mdp.tprob\n",
- "\n",
- " oob_count = sum(!inbounds(mdp, n) for n in neighbors) # number of out of bounds neighbors\n",
- "\n",
- " new_probability = (1.0 - mdp.tprob)/(3-oob_count)\n",
- "\n",
- " for i = 1:4 # do not include neighbor 5\n",
- " if inbounds(mdp, neighbors[i]) && i != target\n",
- " probability[i] = new_probability\n",
- " end\n",
- " end\n",
- " end\n",
- "\n",
- " return SparseCat(neighbors, probability)\n",
- "end;"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "> Performance Note: It is inefficient to create mutable objects like dictionaries and vectors in low-level code like the `transition` function because it requires dynamic memory allocation. This code is written for clarity rather than speed. Better speed could be realized by putting the Dict in the mdp object or using if statements instead, and replacing the vector with a [`StaticArrays.Svector`](https://github.com/JuliaArrays/StaticArrays.jl). However, a much more important consideration for performance is [type stability](https://en.wikibooks.org/wiki/Introducing_Julia/Types#Type_stability), which this function maintains because it always returns a `SparseCat{Vector{GridWorldState},Vector{Float64}}` object."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Reward Model\n",
- "The reward model $R(s,a,s')$ is a function that returns the reward of being in state $s$, taking an action $a$ from that state, and ending up in state $s'$. In our problem, we are rewarded for reaching a terimanl reward state (this could be positive or negative)."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 11,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "function POMDPs.reward(mdp::GridWorld, state::GridWorldState, action::Symbol, statep::GridWorldState) #deleted action\n",
- " if state.done\n",
- " return 0.0\n",
- " end\n",
- " r = 0.0\n",
- " n = length(mdp.reward_states)\n",
- " for i = 1:n\n",
- " if posequal(state, mdp.reward_states[i])\n",
- " r += mdp.reward_values[i]\n",
- " end\n",
- " end\n",
- " return r\n",
- "end;\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Miscallenous Functions\n",
- "We are almost done! Just a few simple functions left. First let's implement two functions that return the sizes of our state and action spaces."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 12,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "POMDPs.n_states(mdp::GridWorld) = 2*mdp.size_x*mdp.size_y\n",
- "POMDPs.n_actions(mdp::GridWorld) = 4"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Now, we implement the discount function."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 13,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "POMDPs.discount(mdp::GridWorld) = mdp.discount_factor;"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "The last thing we need is indexing functions. This allows us to index between the discrete utility array and the states and actions in our problem. We will use the ```sub2ind()``` function from Julia base to help us here."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 14,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "function POMDPs.state_index(mdp::GridWorld, state::GridWorldState)\n",
- " sd = Int(state.done + 1)\n",
- " return sub2ind((mdp.size_x, mdp.size_y, 2), state.x, state.y, sd)\n",
- "end\n",
- "function POMDPs.action_index(mdp::GridWorld, act::Symbol)\n",
- " if act==:up\n",
- " return 1\n",
- " elseif act==:down\n",
- " return 2\n",
- " elseif act==:left\n",
- " return 3\n",
- " elseif act==:right\n",
- " return 4\n",
- " end\n",
- " error(\"Invalid GridWorld action: $act\")\n",
- "end;"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Finally let's define a function that checks if a state is terminal."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 15,
- "metadata": {
- "collapsed": true
- },
- "outputs": [],
- "source": [
- "POMDPs.isterminal(mdp::GridWorld, s::GridWorldState) = s.done"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "# Simulations\n",
- "\n",
- "Now that we have defined the problem, we should simulate it to see it working. The funcion `sim(::MDP)` from `POMDPToolbox` provides a convenient `do` block syntax for exploring the behavior of the mdp. The `do` block receives the state as the argument and should return an action. In this way it acts as a \"hook\" into the simulation and allows quick ad-hoc policies to be defined."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 16,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "state is: GridWorldState(4, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(5, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(6, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(7, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(8, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(9, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(10, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(10, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(10, 1, false)\n",
- "moving right\n",
- "state is: GridWorldState(10, 1, false)\n",
- "moving right\n"
- ]
- }
- ],
- "source": [
- "mdp = GridWorld()\n",
- "mdp.tprob=1.0\n",
- "sim(mdp, GridWorldState(4,1), max_steps=10) do s\n",
- " println(\"state is: $s\")\n",
- " a = :right\n",
- " println(\"moving $a\")\n",
- " return a\n",
- "end;"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Value Iteration Solver"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Value iteration is a dynamic porgramming apporach for solving MDPs. See the [wikipedia](https://en.wikipedia.org/wiki/Markov_decision_process#Value_iteration) article for a brief explanation. The solver can be found [here](https://github.com/JuliaPOMDP/DiscreteValueIteration.jl). If you haven't isntalled the solver yet, you can run the following from the Julia REPL to download the module."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "```julia\n",
- "POMDPs.add(\"DiscreteValueIteration\")\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Each POMDPs.jl solver provides two data types for you to interface with. The first is the Solver type which contains solver parameters. The second is the Policy type. Let's see hwo we can use them to get an optimal action at a given state."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 17,
- "metadata": {
- "collapsed": false,
- "scrolled": false
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "[Iteration 1 ] residual: 10 | iteration runtime: 0.493 ms, ( 0.000493 s total)\n",
- "[Iteration 2 ] residual: 6.3 | iteration runtime: 0.570 ms, ( 0.00106 s total)\n",
- "[Iteration 3 ] residual: 4.54 | iteration runtime: 0.490 ms, ( 0.00155 s total)\n",
- "[Iteration 4 ] residual: 3.39 | iteration runtime: 0.506 ms, ( 0.00206 s total)\n",
- "[Iteration 5 ] residual: 2.57 | iteration runtime: 0.489 ms, ( 0.00255 s total)\n",
- "[Iteration 6 ] residual: 1.92 | iteration runtime: 0.491 ms, ( 0.00304 s total)\n",
- "[Iteration 7 ] residual: 1.39 | iteration runtime: 0.496 ms, ( 0.00354 s total)\n",
- "[Iteration 8 ] residual: 1.07 | iteration runtime: 0.492 ms, ( 0.00403 s total)\n",
- "[Iteration 9 ] residual: 0.861 | iteration runtime: 0.499 ms, ( 0.00453 s total)\n",
- "[Iteration 10 ] residual: 0.662 | iteration runtime: 0.491 ms, ( 0.00502 s total)\n",
- "[Iteration 11 ] residual: 0.489 | iteration runtime: 0.499 ms, ( 0.00552 s total)\n",
- "[Iteration 12 ] residual: 0.405 | iteration runtime: 0.530 ms, ( 0.00605 s total)\n",
- "[Iteration 13 ] residual: 0.341 | iteration runtime: 0.520 ms, ( 0.00657 s total)\n",
- "[Iteration 14 ] residual: 0.244 | iteration runtime: 0.537 ms, ( 0.0071 s total)\n",
- "[Iteration 15 ] residual: 0.166 | iteration runtime: 0.511 ms, ( 0.00761 s total)\n",
- "[Iteration 16 ] residual: 0.106 | iteration runtime: 0.498 ms, ( 0.00811 s total)\n",
- "[Iteration 17 ] residual: 0.0638 | iteration runtime: 0.487 ms, ( 0.0086 s total)\n",
- "[Iteration 18 ] residual: 0.0369 | iteration runtime: 0.487 ms, ( 0.00909 s total)\n",
- "[Iteration 19 ] residual: 0.0208 | iteration runtime: 0.553 ms, ( 0.00964 s total)\n",
- "[Iteration 20 ] residual: 0.0115 | iteration runtime: 0.485 ms, ( 0.0101 s total)\n",
- "[Iteration 21 ] residual: 0.00621 | iteration runtime: 0.529 ms, ( 0.0107 s total)\n",
- "[Iteration 22 ] residual: 0.00333 | iteration runtime: 0.527 ms, ( 0.0112 s total)\n",
- "[Iteration 23 ] residual: 0.00177 | iteration runtime: 0.524 ms, ( 0.0117 s total)\n",
- "[Iteration 24 ] residual: 0.000934 | iteration runtime: 0.522 ms, ( 0.0122 s total)\n"
- ]
- }
- ],
- "source": [
- "# first let's load the value iteration module\n",
- "using DiscreteValueIteration\n",
- "\n",
- "# initialize the problem\n",
- "mdp = GridWorld()\n",
- "\n",
- "# initialize the solver\n",
- "# max_iterations: maximum number of iterations value iteration runs for (default is 100)\n",
- "# belres: the value of Bellman residual used in the solver (defualt is 1e-3)\n",
- "solver = ValueIterationSolver(max_iterations=100, belres=1e-3)\n",
- "\n",
- "# initialize the policy by passing in your problem\n",
- "policy = ValueIterationPolicy(mdp) \n",
- "\n",
- "# solve for an optimal policy\n",
- "# if verbose=false, the text output will be supressed (false by default)\n",
- "solve(solver, mdp, policy, verbose=true);"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Now, we can use the policy along with the ```action(...)``` function to get the optimal action in a given state."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 18,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- ":up"
- ]
- },
- "execution_count": 18,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "# say we are in state (9,2)\n",
- "s = GridWorldState(9,2)\n",
- "a = action(policy, s)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Remeber that the state (9,3) has an immediate reward of +10.0, so the policy we found is moving up as expected!"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 19,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/plain": [
- ":right"
- ]
- },
- "execution_count": 19,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "s = GridWorldState(8,3)\n",
- "a = action(policy, s)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- ""
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## Monte-Carlo Tree Search Solver\n",
- "Monte-Carlo Tree Search (MCTS) is another MDP solver. It is an online method that looks for the best action from only the current state by building a search tree. A nice overview of MCTS can be found [here](http://pubs.doc.ic.ac.uk/survey-mcts-methods/survey-mcts-methods.pdf). Run the following command to donwload the module\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "```julia\n",
- "POMDPs.add(\"MCTS\")\n",
- "```"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Let's quickly run through an example of using the solver:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 20,
- "metadata": {
- "collapsed": false,
- "scrolled": true
- },
- "outputs": [
- {
- "name": "stderr",
- "output_type": "stream",
- "text": [
- "\u001b[1m\u001b[36mINFO: \u001b[39m\u001b[22m\u001b[36mLoading HttpServer methods...\n",
- "\u001b[39m"
- ]
- },
- {
- "data": {
- "text/plain": [
- ":up"
- ]
- },
- "execution_count": 20,
- "metadata": {},
- "output_type": "execute_result"
- }
- ],
- "source": [
- "using MCTS\n",
- "\n",
- "# initialize the problem\n",
- "mdp = GridWorld()\n",
- "\n",
- "# initialize the solver with hyper parameters\n",
- "# n_iterations: the number of iterations that each search runs for\n",
- "# depth: the depth of the tree (how far away from the current state the algorithm explores)\n",
- "# exploration constant: this is how much weight to put into exploratory actions. \n",
- "# A good rule of thumb is to set the exploration constant to what you expect the upper bound on your average expected reward to be.\n",
- "solver = MCTSSolver(n_iterations=1000,\n",
- " depth=20,\n",
- " exploration_constant=10.0,\n",
- " enable_tree_vis=true)\n",
- "\n",
- "# initialize the planner by calling the `solve` function. For online solvers, the \n",
- "planner = solve(solver, mdp)\n",
- "\n",
- "# to get the action:\n",
- "s = GridWorldState(9,2)\n",
- "a = action(planner, s)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "collapsed": true
- },
- "source": [
- "Let's simulate using the planner to determine a good action at each timestep."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 21,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "Total discounted reward: 4.782969000000001\n"
- ]
- }
- ],
- "source": [
- "# we'll use POMDPToolbox for simulation\n",
- "using POMDPToolbox # if you don't have this module install it by running POMDPs.add(\"POMDPToolbox\")\n",
- "\n",
- "s = GridWorldState(4,1) # this is our starting state\n",
- "hist = HistoryRecorder(max_steps=1000)\n",
- "\n",
- "hist = simulate(hist, mdp, policy, s)\n",
- "\n",
- "println(\"Total discounted reward: $(discounted_reward(hist))\")"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "Now we can view the state-action history using the `eachstep` funciton."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 22,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "name": "stdout",
- "output_type": "stream",
- "text": [
- "s: GridWorldState(4, 1, false) a: right s': GridWorldState(5, 1, false)\n",
- "s: GridWorldState(5, 1, false) a: right s': GridWorldState(5, 2, false)\n",
- "s: GridWorldState(5, 2, false) a: right s': GridWorldState(6, 2, false)\n",
- "s: GridWorldState(6, 2, false) a: right s': GridWorldState(7, 2, false)\n",
- "s: GridWorldState(7, 2, false) a: right s': GridWorldState(7, 3, false)\n",
- "s: GridWorldState(7, 3, false) a: right s': GridWorldState(8, 3, false)\n",
- "s: GridWorldState(8, 3, false) a: right s': GridWorldState(9, 3, false)\n",
- "s: GridWorldState(9, 3, false) a: up s': GridWorldState(9, 3, true)\n"
- ]
- }
- ],
- "source": [
- "for (s, a, sp) in eachstep(hist, \"s,a,sp\")\n",
- " @printf(\"s: %-26s a: %-6s s': %-26s\\n\", s, a, sp)\n",
- "end"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "To see what the planner is doing, we can look at the tree created when it plans at a particular state, for example, the first state in the history."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 23,
- "metadata": {
- "collapsed": false
- },
- "outputs": [
- {
- "data": {
- "text/html": [
- " \n",
- " \n",
- " \n",
- " \n",
- " MCTS tree\n",
- " \n",
- " \n",
- " \n",
- " \n",
- " \n",
- "
\n",
- " Attempting to display the tree. If the tree is large, this may take some time.\n",
- "
\n",
- "
\n",
- " Note: D3Trees.jl requires an internet connection. If no tree appears, please check your connection. To help fix this, please see this issue. You may also diagnose errors with the javascript console (Ctrl-Shift-J in chrome).\n",
- "
\n",
- "
\n",
+ " \n",
+ " \n",
+ "
\n",
+ " Attempting to display the tree. If the tree is large, this may take some time.\n",
+ "
\n",
+ "
\n",
+ " Note: D3Trees.jl requires an internet connection. If no tree appears, please check your connection. To help fix this, please see this issue. You may also diagnose errors with the javascript console (Ctrl-Shift-J in chrome).\n",
+ "
\n",
+ "