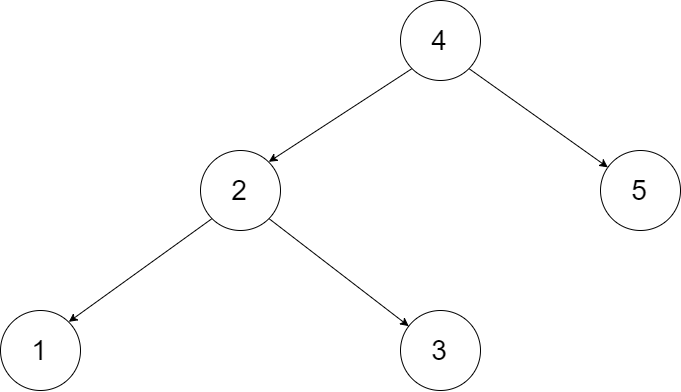
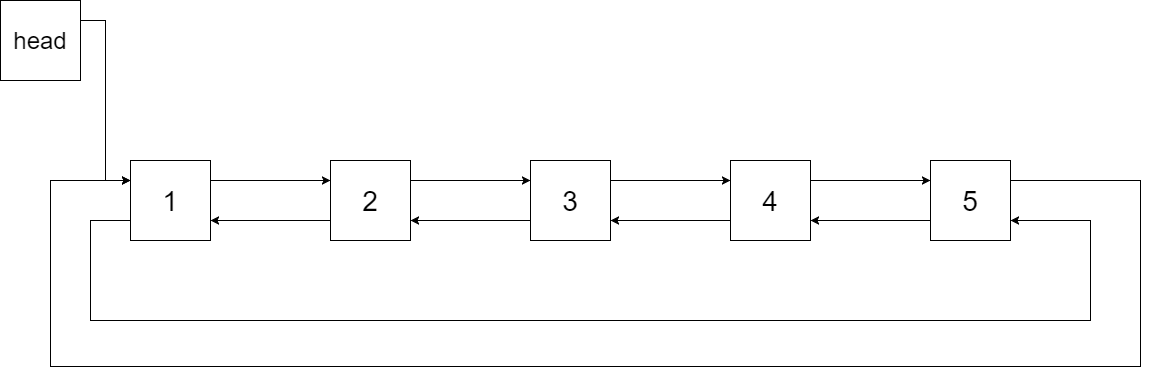
Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.
You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.
We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.
Example 1:
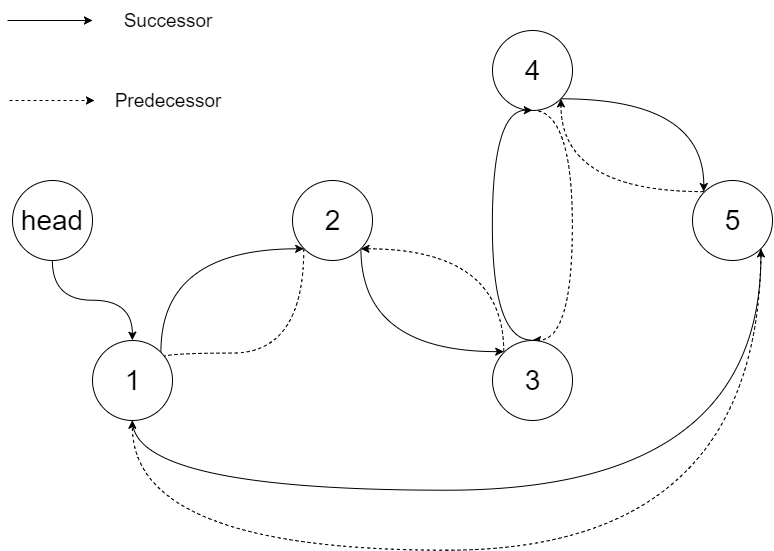
Input: root = [4,2,5,1,3]Output: [1,2,3,4,5] Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.
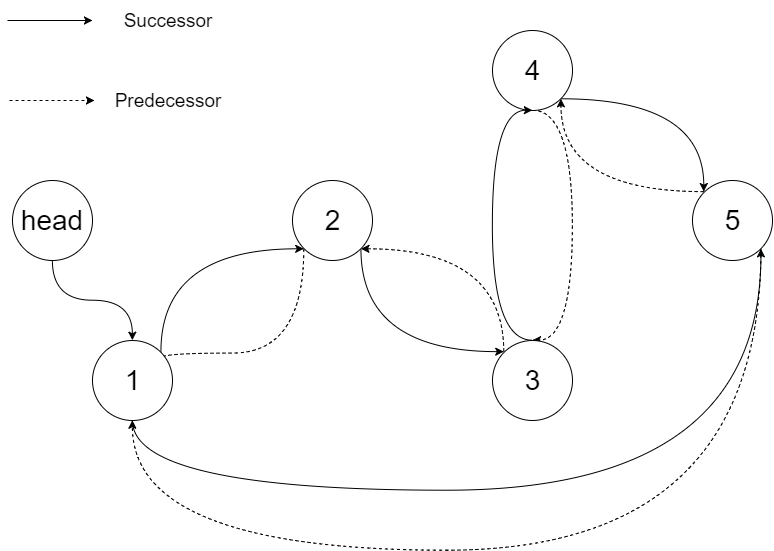
Example 2:
Input: root = [2,1,3] Output: [1,2,3]
Example 3:
Input: root = [] Output: [] Explanation: Input is an empty tree. Output is also an empty Linked List.
Example 4:
Input: root = [1] Output: [1]
Constraints:
-1000 <= Node.val <= 1000Node.left.val < Node.val < Node.right.val- All values of
Node.valare unique. 0 <= Number of Nodes <= 2000
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
def dfs(cur):
if cur is None:
return
dfs(cur.left)
if self.pre is None:
self.head = cur
else:
self.pre.right = cur
cur.left = self.pre
self.pre = cur
dfs(cur.right)
if root is None:
return None
self.head = self.pre = None
dfs(root)
self.head.left = self.pre
self.pre.right = self.head
return self.head/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
private Node head;
private Node pre;
public Node treeToDoublyList(Node root) {
if (root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
private void dfs(Node cur) {
if (cur == null) return;
dfs(cur.left);
if (pre == null) head = cur;
else pre.right = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}/**
* // Definition for a Node.
* function Node(val,left,right) {
* this.val = val;
* this.left = left;
* this.right = right;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var treeToDoublyList = function (root) {
function dfs(cur) {
if (!cur) return;
dfs(cur.left);
if (!pre) head = cur;
else pre.right = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
if (!root) return null;
let head, pre;
dfs(root);
head.left = pre;
pre.right = head;
return head;
};