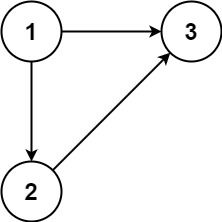
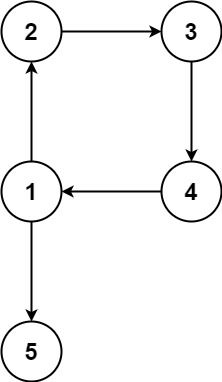
在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
示例 1:
输入:edges = [[1,2],[1,3],[2,3]] 输出:[2,3]
示例 2:
输入:edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] 输出:[4,1]
提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ui, vi <= n
方法一:并查集
有两个入度时,当一条边被记为 conflict,就相当于删掉了这条边,因为并没有调用并查集 union 进行合并,如果还出现了无向环,则说明是要删另一条入度的边。
每个节点都只有一个入度时,则说明是一个有向环,删最后一条出现的边即可。
class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.n = n
def union(self, a, b):
if self.find(a) == self.find(b):
return False
self.p[self.find(a)] = self.find(b)
self.n -= 1
return True
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
class Solution:
def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
p = list(range(n + 1))
uf = UnionFind(n + 1)
conflict = cycle = None
for i, (u, v) in enumerate(edges):
if p[v] != v:
conflict = i
else:
p[v] = u
if not uf.union(u, v):
cycle = i
if conflict is None:
return edges[cycle]
v = edges[conflict][1]
if cycle is not None:
return [p[v], v]
return edges[conflict]class Solution {
public int[] findRedundantDirectedConnection(int[][] edges) {
int n = edges.length;
int[] p = new int[n + 1];
for (int i = 0; i <= n; ++i) {
p[i] = i;
}
UnionFind uf = new UnionFind(n + 1);
int conflict = -1, cycle = -1;
for (int i = 0; i < n; ++i) {
int u = edges[i][0], v = edges[i][1];
if (p[v] != v) {
conflict = i;
} else {
p[v] = u;
if (!uf.union(u, v)) {
cycle = i;
}
}
}
if (conflict == -1) {
return edges[cycle];
}
int v = edges[conflict][1];
if (cycle != -1) {
return new int[] {p[v], v};
}
return edges[conflict];
}
}
class UnionFind {
public int[] p;
public int n;
public UnionFind(int n) {
p = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
}
this.n = n;
}
public boolean union(int a, int b) {
int pa = find(a);
int pb = find(b);
if (pa == pb) {
return false;
}
p[pa] = pb;
--n;
return true;
}
public int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class UnionFind {
public:
vector<int> p;
int n;
UnionFind(int _n)
: n(_n)
, p(_n) {
iota(p.begin(), p.end(), 0);
}
bool unite(int a, int b) {
int pa = find(a), pb = find(b);
if (pa == pb) return false;
p[pa] = pb;
--n;
return true;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};
class Solution {
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> p(n + 1);
for (int i = 0; i <= n; ++i) p[i] = i;
UnionFind uf(n + 1);
int conflict = -1, cycle = -1;
for (int i = 0; i < n; ++i) {
int u = edges[i][0], v = edges[i][1];
if (p[v] != v)
conflict = i;
else {
p[v] = u;
if (!uf.unite(u, v)) cycle = i;
}
}
if (conflict == -1) return edges[cycle];
int v = edges[conflict][1];
if (cycle != -1) return {p[v], v};
return edges[conflict];
}
};type unionFind struct {
p []int
n int
}
func newUnionFind(n int) *unionFind {
p := make([]int, n)
for i := range p {
p[i] = i
}
return &unionFind{p, n}
}
func (uf *unionFind) find(x int) int {
if uf.p[x] != x {
uf.p[x] = uf.find(uf.p[x])
}
return uf.p[x]
}
func (uf *unionFind) union(a, b int) bool {
if uf.find(a) == uf.find(b) {
return false
}
uf.p[uf.find(a)] = uf.find(b)
uf.n--
return true
}
func findRedundantDirectedConnection(edges [][]int) []int {
n := len(edges)
p := make([]int, n+1)
for i := range p {
p[i] = i
}
uf := newUnionFind(n + 1)
conflict, cycle := -1, -1
for i, e := range edges {
u, v := e[0], e[1]
if p[v] != v {
conflict = i
} else {
p[v] = u
if !uf.union(u, v) {
cycle = i
}
}
}
if conflict == -1 {
return edges[cycle]
}
v := edges[conflict][1]
if cycle != -1 {
return []int{p[v], v}
}
return edges[conflict]
}