Skip to content

Latest commit

 

History

History
392 lines (322 loc) · 11.8 KB

README.md

File metadata and controls

392 lines (322 loc) · 11.8 KB
Raw

1235. 规划兼职工作

English Version

题目描述

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

 

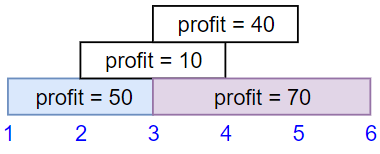
示例 1：

输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作， 
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

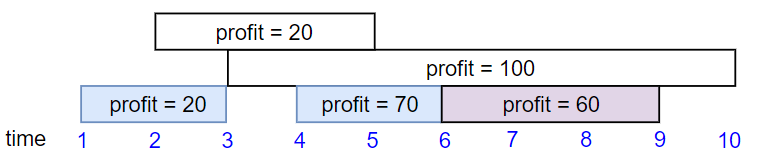
示例 2：

输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。 
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

 

提示：

  • 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
  • 1 <= startTime[i] < endTime[i] <= 10^9
  • 1 <= profit[i] <= 10^4

解法

方法一：记忆化搜索 + 二分查找

我们先将工作按照开始时间从小到大排序，然后设计一个函数 $dfs(i)$ 表示从第 $i$ 份工作开始，可以获得的最大报酬。答案即为 $dfs(0)$。

函数 $dfs(i)$ 的计算过程如下：

对于第 $i$ 份工作，我们可以选择做，也可以选择不做。如果不做，最大报酬就是 $dfs(i + 1)$；如果做，我们可以通过二分查找，找到在第 $i$ 份工作结束时间之后开始的第一份工作，记为 $j$，那么最大报酬就是 $profit[i] + dfs(j)$。取两者的较大值即可。即：

$$ dfs(i)=\max(dfs(i+1),profit[i]+dfs(j)) $$

其中 $j$ 是满足 $startTime[j] \ge endTime[i]$ 的最小的下标。

此过程中，我们可以使用记忆化搜索，将每个状态的答案保存下来，避免重复计算。

时间复杂度 $O(n \times \log n)$，其中 $n$ 是工作的数量。

方法二：动态规划 + 二分查找

我们还可以将方法一中的记忆化搜索改为动态规划。

先将工作排序，这次我们按照结束时间从小到大排序，然后定义 $dp[i]$，表示前 $i$ 份工作中，可以获得的最大报酬。答案即为 $dp[n]$。初始化 $dp[0]=0$。

对于第 $i$ 份工作，我们可以选择做，也可以选择不做。如果不做，最大报酬就是 $dp[i]$；如果做，我们可以通过二分查找，找到在第 $i$ 份工作开始时间之前结束的最后一份工作，记为 $j$，那么最大报酬就是 $profit[i] + dp[j]$。取两者的较大值即可。即：

$$ dp[i+1] = \max(dp[i], profit[i] + dp[j]) $$

其中 $j$ 是满足 $endTime[j] \leq startTime[i]$ 的最大的下标。

时间复杂度 $O(n \times \log n)$，其中 $n$ 是工作的数量。

相似题目：

Python3

class Solution:
    def jobScheduling(
        self, startTime: List[int], endTime: List[int], profit: List[int]
    ) -> int:
        @cache
        def dfs(i):
            if i >= n:
                return 0
            _, e, p = jobs[i]
            j = bisect_left(jobs, e, lo=i + 1, key=lambda x: x[0])
            return max(dfs(i + 1), p + dfs(j))

        jobs = sorted(zip(startTime, endTime, profit))
        n = len(profit)
        return dfs(0)
class Solution:
    def jobScheduling(
        self, startTime: List[int], endTime: List[int], profit: List[int]
    ) -> int:
        @cache
        def dfs(i: int) -> int:
            if i >= n:
                return 0
            j = bisect_left(idx, endTime[idx[i]], key=lambda i: startTime[i])
            return max(dfs(i + 1), profit[idx[i]] + dfs(j))

        n = len(startTime)
        idx = sorted(range(n), key=lambda i: startTime[i])
        return dfs(0)
class Solution:
    def jobScheduling(
        self, startTime: List[int], endTime: List[int], profit: List[int]
    ) -> int:
        jobs = sorted(zip(endTime, startTime, profit))
        n = len(profit)
        dp = [0] * (n + 1)
        for i, (_, s, p) in enumerate(jobs):
            j = bisect_right(jobs, s, hi=i, key=lambda x: x[0])
            dp[i + 1] = max(dp[i], dp[j] + p)
        return dp[n]

Java

class Solution {
    private int[][] jobs;
    private int[] f;
    private int n;

    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        n = profit.length;
        jobs = new int[n][3];
        for (int i = 0; i < n; ++i) {
            jobs[i] = new int[] {startTime[i], endTime[i], profit[i]};
        }
        Arrays.sort(jobs, (a, b) -> a[0] - b[0]);
        f = new int[n];
        return dfs(0);
    }

    private int dfs(int i) {
        if (i >= n) {
            return 0;
        }
        if (f[i] != 0) {
            return f[i];
        }
        int e = jobs[i][1], p = jobs[i][2];
        int j = search(jobs, e, i + 1);
        int ans = Math.max(dfs(i + 1), p + dfs(j));
        f[i] = ans;
        return ans;
    }

    private int search(int[][] jobs, int x, int i) {
        int left = i, right = n;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (jobs[mid][0] >= x) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}
class Solution {
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int n = profit.length;
        int[][] jobs = new int[n][3];
        for (int i = 0; i < n; ++i) {
            jobs[i] = new int[] {startTime[i], endTime[i], profit[i]};
        }
        Arrays.sort(jobs, (a, b) -> a[1] - b[1]);
        int[] dp = new int[n + 1];
        for (int i = 0; i < n; ++i) {
            int j = search(jobs, jobs[i][0], i);
            dp[i + 1] = Math.max(dp[i], dp[j] + jobs[i][2]);
        }
        return dp[n];
    }

    private int search(int[][] jobs, int x, int n) {
        int left = 0, right = n;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (jobs[mid][1] > x) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

C++

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = profit.size();
        vector<tuple<int, int, int>> jobs(n);
        for (int i = 0; i < n; ++i) jobs[i] = {startTime[i], endTime[i], profit[i]};
        sort(jobs.begin(), jobs.end());
        vector<int> f(n);
        function<int(int)> dfs = [&](int i) -> int {
            if (i >= n) return 0;
            if (f[i]) return f[i];
            auto [_, e, p] = jobs[i];
            tuple<int, int, int> t{e, 0, 0};
            int j = lower_bound(jobs.begin() + i + 1, jobs.end(), t, [&](auto& l, auto& r) -> bool { return get<0>(l) < get<0>(r); }) - jobs.begin();
            int ans = max(dfs(i + 1), p + dfs(j));
            f[i] = ans;
            return ans;
        };
        return dfs(0);
    }
};
class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = profit.size();
        vector<tuple<int, int, int>> jobs(n);
        for (int i = 0; i < n; ++i) jobs[i] = {endTime[i], startTime[i], profit[i]};
        sort(jobs.begin(), jobs.end());
        vector<int> dp(n + 1);
        for (int i = 0; i < n; ++i) {
            auto [_, s, p] = jobs[i];
            int j = upper_bound(jobs.begin(), jobs.begin() + i, s, [&](int x, auto& job) -> bool { return x < get<0>(job); }) - jobs.begin();
            dp[i + 1] = max(dp[i], dp[j] + p);
        }
        return dp[n];
    }
};

Go

func jobScheduling(startTime []int, endTime []int, profit []int) int {
	n := len(profit)
	type tuple struct{ s, e, p int }
	jobs := make([]tuple, n)
	for i, p := range profit {
		jobs[i] = tuple{startTime[i], endTime[i], p}
	}
	sort.Slice(jobs, func(i, j int) bool { return jobs[i].s < jobs[j].s })
	f := make([]int, n)
	var dfs func(int) int
	dfs = func(i int) int {
		if i >= n {
			return 0
		}
		if f[i] != 0 {
			return f[i]
		}
		j := sort.Search(n, func(j int) bool { return jobs[j].s >= jobs[i].e })
		ans := max(dfs(i+1), jobs[i].p+dfs(j))
		f[i] = ans
		return ans
	}
	return dfs(0)
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}
func jobScheduling(startTime []int, endTime []int, profit []int) int {
	n := len(profit)
	type tuple struct{ s, e, p int }
	jobs := make([]tuple, n)
	for i, p := range profit {
		jobs[i] = tuple{startTime[i], endTime[i], p}
	}
	sort.Slice(jobs, func(i, j int) bool { return jobs[i].e < jobs[j].e })
	dp := make([]int, n+1)
	for i, job := range jobs {
		j := sort.Search(i, func(k int) bool { return jobs[k].e > job.s })
		dp[i+1] = max(dp[i], dp[j]+job.p)
	}
	return dp[n]
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

TypeScript

function jobScheduling(
    startTime: number[],
    endTime: number[],
    profit: number[],
): number {
    const n = startTime.length;
    const f = new Array(n).fill(0);
    const idx = new Array(n).fill(0).map((_, i) => i);
    idx.sort((i, j) => startTime[i] - startTime[j]);
    const search = (x: number) => {
        let l = 0;
        let r = n;
        while (l < r) {
            const mid = (l + r) >> 1;
            if (startTime[idx[mid]] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    };
    const dfs = (i: number): number => {
        if (i >= n) {
            return 0;
        }
        if (f[i] !== 0) {
            return f[i];
        }
        const j = search(endTime[idx[i]]);
        return (f[i] = Math.max(dfs(i + 1), dfs(j) + profit[idx[i]]));
    };
    return dfs(0);
}

...