Skip to content

Latest commit

 

History

History
568 lines (483 loc) · 15.5 KB

README.md

File metadata and controls

568 lines (483 loc) · 15.5 KB
Raw

1631. 最小体力消耗路径

English Version

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

 

示例 1：

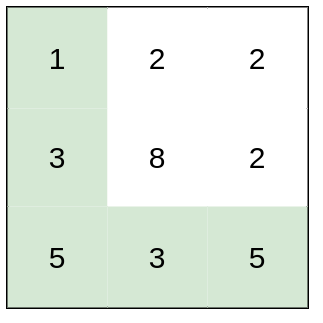
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

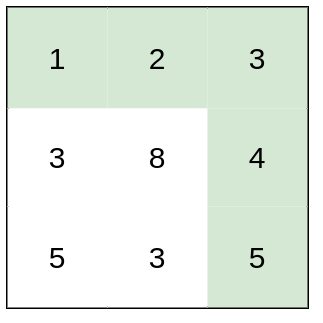
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

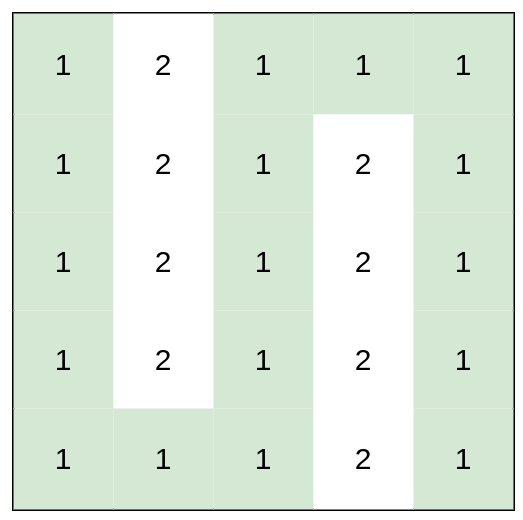
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

 

提示：

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

解法

方法一：并查集

对于本题，每个格子当做图的一个节点，把相邻两个格子的高度差绝对值当做边的权重，因此本题是求解从最左上角的节点到最右下角的节点的连通性问题。

先把图中所有边去掉，然后按照边的权重从小到大，逐个把边添加上。如果在某一次添加一条边时，最左上角和最右下角的节点连通了，那么该边的权重就是题目的最小体力消耗值。

并查集模板：

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))


# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n


# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n


# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]


# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

方法二：二分查找 + BFS

二分枚举体力消耗值，用 BFS 找到满足条件的最小消耗值即可。

方法三：堆优化版 Dijkstra 算法

时间复杂度 O(mlogn)。

Python3

并查集：

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        m, n = len(heights), len(heights[0])
        p = list(range(m * n))
        e = []
        for i in range(m):
            for j in range(n):
                if i < m - 1:
                    e.append(
                        (
                            abs(heights[i][j] - heights[i + 1][j]),
                            i * n + j,
                            (i + 1) * n + j,
                        )
                    )
                if j < n - 1:
                    e.append(
                        (
                            abs(heights[i][j] - heights[i][j + 1]),
                            i * n + j,
                            i * n + j + 1,
                        )
                    )
        e.sort()
        for h, i, j in e:
            p[find(i)] = find(j)
            if find(0) == find(m * n - 1):
                return h
        return 0

二分查找 + BFS：

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        m, n = len(heights), len(heights[0])
        left, right = 0, 999999
        while left < right:
            mid = (left + right) >> 1
            q = deque([(0, 0)])
            vis = {(0, 0)}
            while q:
                i, j = q.popleft()
                for a, b in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                    x, y = i + a, j + b
                    if (
                        0 <= x < m
                        and 0 <= y < n
                        and (x, y) not in vis
                        and abs(heights[i][j] - heights[x][y]) <= mid
                    ):
                        q.append((x, y))
                        vis.add((x, y))
            if (m - 1, n - 1) in vis:
                right = mid
            else:
                left = mid + 1
        return left

Dijkstra 算法：

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        INF = 0x3F3F3F3F
        m, n = len(heights), len(heights[0])
        dist = [[INF] * n for _ in range(m)]
        dist[0][0] = 0
        dirs = [-1, 0, 1, 0, -1]
        q = [(0, 0, 0)]
        while q:
            t, i, j = heappop(q)
            for k in range(4):
                x, y = i + dirs[k], j + dirs[k + 1]
                if (
                    0 <= x < m
                    and 0 <= y < n
                    and max(t, abs(heights[x][y] - heights[i][j])) < dist[x][y]
                ):
                    dist[x][y] = max(t, abs(heights[x][y] - heights[i][j]))
                    heappush(q, (dist[x][y], x, y))
        return dist[-1][-1]

Java

并查集：

class Solution {
    private int[] p;

    public int minimumEffortPath(int[][] heights) {
        int m = heights.length;
        int n = heights[0].length;
        p = new int[m * n];
        for (int i = 0; i < p.length; ++i) {
            p[i] = i;
        }
        List<int[]> edges = new ArrayList<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i < m - 1) {
                    edges.add(new int[] {
                        Math.abs(heights[i][j] - heights[i + 1][j]), i * n + j, (i + 1) * n + j});
                }
                if (j < n - 1) {
                    edges.add(new int[] {
                        Math.abs(heights[i][j] - heights[i][j + 1]), i * n + j, i * n + j + 1});
                }
            }
        }
        Collections.sort(edges, Comparator.comparingInt(a -> a[0]));
        for (int[] e : edges) {
            int i = e[1], j = e[2];
            p[find(i)] = find(j);
            if (find(0) == find(m * n - 1)) {
                return e[0];
            }
        }
        return 0;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

二分查找 + BFS：

class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length;
        int n = heights[0].length;
        int left = 0;
        int right = 999999;
        int[] dirs = {-1, 0, 1, 0, -1};
        while (left < right) {
            int mid = (left + right) >> 1;
            boolean[][] vis = new boolean[m][n];
            vis[0][0] = true;
            Deque<int[]> q = new ArrayDeque<>();
            q.offer(new int[] {0, 0});
            while (!q.isEmpty()) {
                int[] p = q.poll();
                int i = p[0], j = p[1];
                for (int k = 0; k < 4; ++k) {
                    int x = i + dirs[k], y = j + dirs[k + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]
                        && Math.abs(heights[i][j] - heights[x][y]) <= mid) {
                        q.offer(new int[] {x, y});
                        vis[x][y] = true;
                    }
                }
            }
            if (vis[m - 1][n - 1]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

Dijkstra 算法：

class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length;
        int n = heights[0].length;
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(dist[i], 0x3f3f3f3f);
        }
        dist[0][0] = 0;
        PriorityQueue<int[]> q = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        q.offer(new int[] {0, 0, 0});
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int t = p[0], i = p[1], j = p[2];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n) {
                    int nd = Math.max(t, Math.abs(heights[x][y] - heights[i][j]));
                    if (nd < dist[x][y]) {
                        dist[x][y] = nd;
                        q.offer(new int[] {nd, x, y});
                    }
                }
            }
        }
        return dist[m - 1][n - 1];
    }
}

C++

并查集：

class Solution {
public:
    vector<int> p;

    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size(), n = heights[0].size();
        p.resize(m * n);
        for (int i = 0; i < p.size(); ++i) p[i] = i;
        vector<vector<int>> edges;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i < m - 1) edges.push_back({abs(heights[i][j] - heights[i + 1][j]), i * n + j, (i + 1) * n + j});
                if (j < n - 1) edges.push_back({abs(heights[i][j] - heights[i][j + 1]), i * n + j, i * n + j + 1});
            }
        }
        sort(edges.begin(), edges.end());
        for (auto& e : edges) {
            int i = e[1], j = e[2];
            p[find(i)] = find(j);
            if (find(0) == find(m * n - 1)) return e[0];
        }
        return 0;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

二分查找 + BFS：

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size(), n = heights[0].size();
        int left = 0, right = 999999;
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (left < right) {
            int mid = (left + right) >> 1;
            vector<vector<bool>> vis(m, vector<bool>(n));
            vis[0][0] = true;
            queue<pair<int, int>> q;
            q.push({0, 0});
            while (!q.empty()) {
                auto [i, j] = q.front();
                q.pop();
                for (int k = 0; k < 4; ++k) {
                    int x = i + dirs[k], y = j + dirs[k + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && abs(heights[i][j] - heights[x][y]) <= mid) {
                        q.push({x, y});
                        vis[x][y] = true;
                    }
                }
            }
            if (vis[m - 1][n - 1])
                right = mid;
            else
                left = mid + 1;
        }
        return left;
    }
};

Dijkstra 算法：

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size(), n = heights[0].size();
        vector<vector<int>> dist(m, vector<int>(n, 0x3f3f3f3f));
        dist[0][0] = 0;
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> q;
        q.push({0, 0, 0});
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto [t, i, j] = q.top();
            q.pop();
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n) {
                    int nd = max(t, abs(heights[x][y] - heights[i][j]));
                    if (nd < dist[x][y]) {
                        dist[x][y] = nd;
                        q.push({nd, x, y});
                    }
                }
            }
        }
        return dist[m - 1][n - 1];
    }
};

Go

并查集：

func minimumEffortPath(heights [][]int) int {
	m, n := len(heights), len(heights[0])
	p := make([]int, m*n)
	for i := range p {
		p[i] = i
	}
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	edges := [][]int{}
	for i, row := range heights {
		for j, h := range row {
			if i < m-1 {
				s := []int{abs(h - heights[i+1][j]), i*n + j, (i+1)*n + j}
				edges = append(edges, s)
			}
			if j < n-1 {
				s := []int{abs(h - row[j+1]), i*n + j, i*n + j + 1}
				edges = append(edges, s)
			}
		}
	}
	sort.Slice(edges, func(i, j int) bool {
		return edges[i][0] < edges[j][0]
	})
	for _, e := range edges {
		i, j := e[1], e[2]
		p[find(i)] = find(j)
		if find(0) == find(m*n-1) {
			return e[0]
		}
	}
	return 0
}

func abs(x int) int {
	if x > 0 {
		return x
	}
	return -x
}

二分查找 + BFS：

func minimumEffortPath(heights [][]int) int {
	m, n := len(heights), len(heights[0])
	left, right := 0, 999999
	dirs := []int{-1, 0, 1, 0, -1}
	for left < right {
		mid := (left + right) >> 1
		vis := make([][]bool, m)
		for i := range vis {
			vis[i] = make([]bool, n)
		}
		vis[0][0] = true
		q := [][]int{{0, 0}}
		for len(q) > 0 {
			p := q[0]
			q = q[1:]
			i, j := p[0], p[1]
			for k := 0; k < 4; k++ {
				x, y := i+dirs[k], j+dirs[k+1]
				if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && abs(heights[i][j]-heights[x][y]) <= mid {
					q = append(q, []int{x, y})
					vis[x][y] = true
				}
			}
		}
		if vis[m-1][n-1] {
			right = mid
		} else {
			left = mid + 1
		}
	}
	return left
}

func abs(x int) int {
	if x > 0 {
		return x
	}
	return -x
}

...