README.md

2204. 无向图中到环的距离

English Version

题目描述

给定一个正整数 n，表示一个 连通无向图 中的节点数，该图 只包含一个 环。节点编号为 0 ~ n - 1(含)。

你还得到了一个二维整数数组 edges，其中 edges[i] = [node1i, node2i] 表示有一条 双向 边连接图中的 node1i 和 node2i。

两个节点 a 和 b 之间的距离定义为从 a 到 b 所需的 最小边数。

返回一个长度为 n 的整数数组 answer，其中 answer[i] 是第 i 个节点与环中任何节点之间的最小距离。

示例 1:

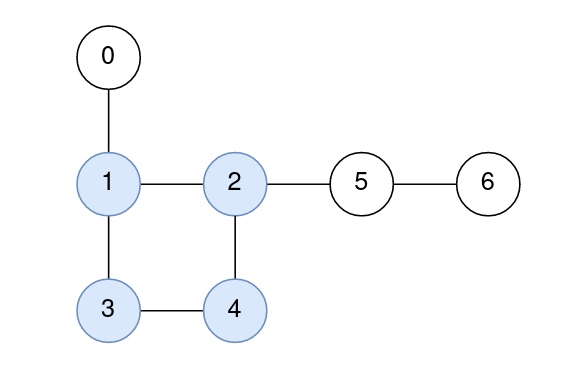
输入: n = 7, edges = [[1,2],[2,4],[4,3],[3,1],[0,1],[5,2],[6,5]]
输出: [1,0,0,0,0,1,2]
解释:
节点 1, 2, 3, 和 4 来自环。
0 到 1 的距离是 1。
1 到 1 的距离是 0。
2 到 2 的距离是 0。
3 到 3 的距离是 0。
4 到 4 的距离是 0。
5 到 2 的距离是 1。
6 到 2 的距离是 2。

示例 2:

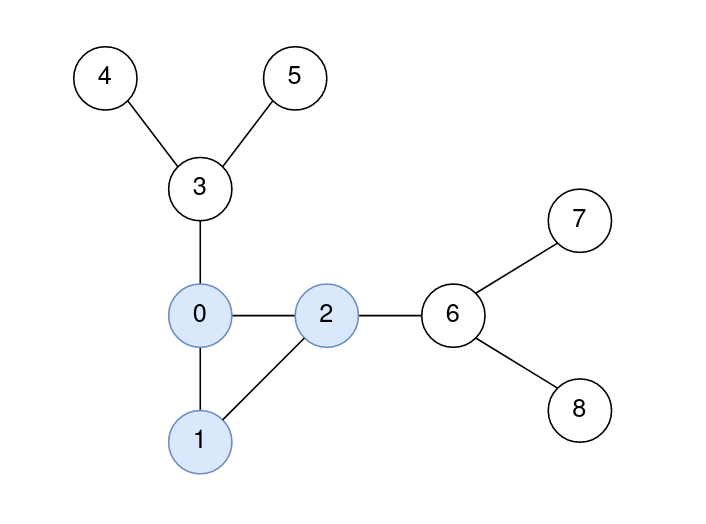
输入: n = 9, edges = [[0,1],[1,2],[0,2],[2,6],[6,7],[6,8],[0,3],[3,4],[3,5]]
输出: [0,0,0,1,2,2,1,2,2]
解释:
节点 0, 1, 和 2 来自环.
0 到 0 的距离是 0。
1 到 1 的距离是 0。
2 到 2 的距离是 0。
3 到 1 的距离是 1。
4 到 1 的距离是 2。
5 到 1 的距离是 2。
6 到 2 的距离是 1。
7 到 2 的距离是 2。
8 到 2 的距离是 2。

 

提示:

• 3 <= n <= 105
• edges.length == n
• edges[i].length == 2
• 0 <= node1i, node2i <= n - 1
• node1i != node2i
• 图是连通的。
• 这个图只有一个环。
• 任何顶点对之间最多只有一条边。

解法

Python3

Java

TypeScript

...