README.md

2257. 统计网格图中没有被保卫的格子数

English Version

题目描述

给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ，其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ，分别表示第 i 个警卫和第 j 座墙所在的位置。

一个警卫能看到 4 个坐标轴方向（即东、南、西、北）的 所有 格子，除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到，那么我们说这个格子被 保卫 了。

请你返回空格子中，有多少个格子是 没被保卫 的。

 

示例 1：

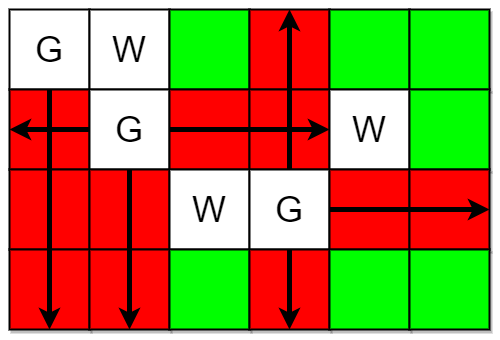
输入：m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
输出：7
解释：上图中，被保卫和没有被保卫的格子分别用红色和绿色表示。
总共有 7 个没有被保卫的格子，所以我们返回 7 。

示例 2：

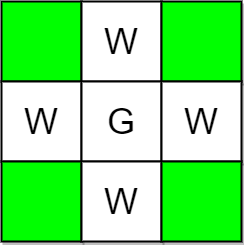
输入：m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
输出：4
解释：上图中，没有被保卫的格子用绿色表示。
总共有 4 个没有被保卫的格子，所以我们返回 4 。

 

提示：

• 1 <= m, n <= 105
• 2 <= m * n <= 105
• 1 <= guards.length, walls.length <= 5 * 104
• 2 <= guards.length + walls.length <= m * n
• guards[i].length == walls[j].length == 2
• 0 <= rowi, rowj < m
• 0 <= coli, colj < n
• guards 和 walls 中所有位置 互不相同 。

解法

方法一：模拟

我们创建一个 $m \times n$ 的二维数组 $g$，其中 $g[i][j]$ 表示第 $i$ 行第 $j$ 列的格子。初始时，$g[i][j]$ 的值为 $0$，表示该格子没有被保卫。

然后遍历所有的警卫和墙，将 $g[i][j]$ 的值置为 $2$，这些位置不能被访问。

接下来，我们遍历所有警卫的位置，从该位置出发，向四个方向进行模拟，直到遇到墙或警卫，或者越界。在模拟的过程中，将遇到的格子的值置为 $1$，表示该格子被保卫。

最后，我们遍历 $g$，统计值为 $0$ 的格子的个数，即为答案。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为网格的行数和列数。

Python3

class Solution:
    def countUnguarded(
        self, m: int, n: int, guards: List[List[int]], walls: List[List[int]]
    ) -> int:
        g = [[0] * n for _ in range(m)]
        for i, j in guards:
            g[i][j] = 2
        for i, j in walls:
            g[i][j] = 2
        dirs = (-1, 0, 1, 0, -1)
        for i, j in guards:
            for a, b in pairwise(dirs):
                x, y = i, j
                while 0 <= x + a < m and 0 <= y + b < n and g[x + a][y + b] < 2:
                    x, y = x + a, y + b
                    g[x][y] = 1
        return sum(v == 0 for row in g for v in row)

Java

class Solution {
    public int countUnguarded(int m, int n, int[][] guards, int[][] walls) {
        int[][] g = new int[m][n];
        for (var e : guards) {
            g[e[0]][e[1]] = 2;
        }
        for (var e : walls) {
            g[e[0]][e[1]] = 2;
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        for (var e : guards) {
            for (int k = 0; k < 4; ++k) {
                int x = e[0], y = e[1];
                int a = dirs[k], b = dirs[k + 1];
                while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) {
                    x += a;
                    y += b;
                    g[x][y] = 1;
                }
            }
        }
        int ans = 0;
        for (var row : g) {
            for (int v : row) {
                if (v == 0) {
                    ++ans;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
        int g[m][n];
        memset(g, 0, sizeof(g));
        for (auto& e : guards) {
            g[e[0]][e[1]] = 2;
        }
        for (auto& e : walls) {
            g[e[0]][e[1]] = 2;
        }
        int dirs[5] = {-1, 0, 1, 0, -1};
        for (auto& e : guards) {
            for (int k = 0; k < 4; ++k) {
                int x = e[0], y = e[1];
                int a = dirs[k], b = dirs[k + 1];
                while (x + a >= 0 && x + a < m && y + b >= 0 && y + b < n && g[x + a][y + b] < 2) {
                    x += a;
                    y += b;
                    g[x][y] = 1;
                }
            }
        }
        int ans = 0;
        for (auto& row : g) {
            ans += count(row, row + n, 0);
        }
        return ans;
    }
};

Go

func countUnguarded(m int, n int, guards [][]int, walls [][]int) (ans int) {
	g := make([][]int, m)
	for i := range g {
		g[i] = make([]int, n)
	}
	for _, e := range guards {
		g[e[0]][e[1]] = 2
	}
	for _, e := range walls {
		g[e[0]][e[1]] = 2
	}
	dirs := [5]int{-1, 0, 1, 0, -1}
	for _, e := range guards {
		for k := 0; k < 4; k++ {
			x, y := e[0], e[1]
			a, b := dirs[k], dirs[k+1]
			for x+a >= 0 && x+a < m && y+b >= 0 && y+b < n && g[x+a][y+b] < 2 {
				x, y = x+a, y+b
				g[x][y] = 1
			}
		}
	}
	for _, row := range g {
		for _, v := range row {
			if v == 0 {
				ans++
			}
		}
	}
	return
}

TypeScript

...