README.md

2320. 统计放置房子的方式数

English Version

题目描述

一条街道上共有 n * 2 个 地块 ，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 109 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

 

示例 1：

输入：n = 1
输出：4
解释：
可能的放置方式：
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子，街道两侧各放置一所。

示例 2：

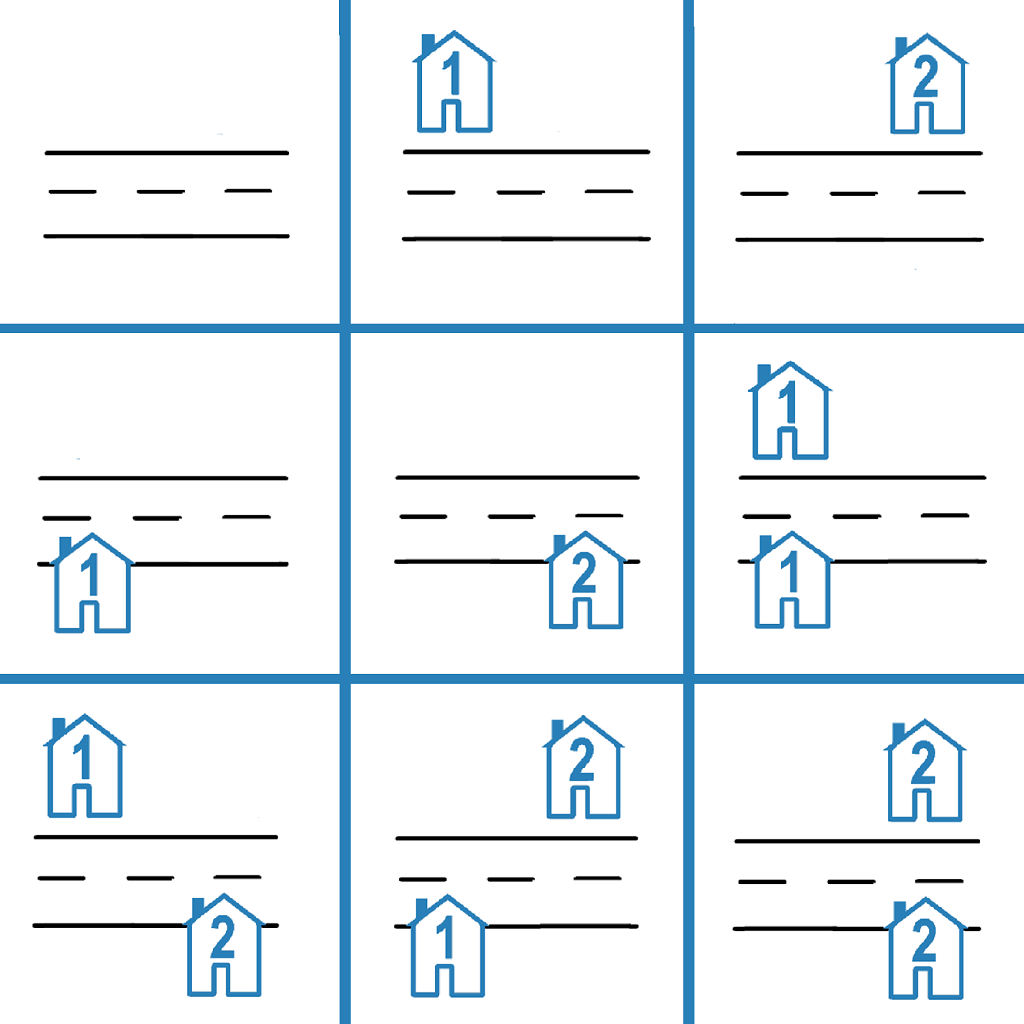
输入：n = 2
输出：9
解释：如上图所示，共有 9 种可能的放置方式。

 

提示：

• 1 <= n <= 104

解法

方法一：动态规划

由于街道两侧房子的摆放互不影响，因此，我们可以只考虑一侧的摆放情况，最后将一侧的方案数平方取模得到最终结果。

我们定义 $f[i]$ 表示放置前 $i+1$ 个地块，且最后一个地块放置房子的方案数，定义 $g[i]$ 表示放置前 $i+1$ 个地块，且最后一个地块不放置房子的方案数。初始时 $f[0] = g[0] = 1$。

当我们放置第 $i+1$ 个地块时，有两种情况：

• 如果第 $i+1$ 个地块放置房子，那么第 $i$ 个地块必须不放置房子，因此方案数 $f[i]=g[i-1]$；
• 如果第 $i+1$ 个地块不放置房子，那么第 $i$ 个地块可以放置房子，也可以不放置房子，因此方案数 $g[i]=f[i-1]+g[i-1]$。

最终，我们将 $f[n-1]+g[n-1]$ 的平方取模即为答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为街道的长度。

Python3

class Solution:
    def countHousePlacements(self, n: int) -> int:
        mod = 10**9 + 7
        f = [1] * n
        g = [1] * n
        for i in range(1, n):
            f[i] = g[i - 1]
            g[i] = (f[i - 1] + g[i - 1]) % mod
        v = f[-1] + g[-1]
        return v * v % mod

Java

class Solution {
    public int countHousePlacements(int n) {
        final int mod = (int) 1e9 + 7;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = 1;
        g[0] = 1;
        for (int i = 1; i < n; ++i) {
            f[i] = g[i - 1];
            g[i] = (f[i - 1] + g[i - 1]) % mod;
        }
        long v = (f[n - 1] + g[n - 1]) % mod;
        return (int) (v * v % mod);
    }
}

C++

class Solution {
public:
    int countHousePlacements(int n) {
        const int mod = 1e9 + 7;
        int f[n], g[n];
        f[0] = g[0] = 1;
        for (int i = 1; i < n; ++i) {
            f[i] = g[i - 1];
            g[i] = (f[i - 1] + g[i - 1]) % mod;
        }
        long v = f[n - 1] + g[n - 1];
        return v * v % mod;
    }
};

Go

func countHousePlacements(n int) int {
	const mod = 1e9 + 7
	f := make([]int, n)
	g := make([]int, n)
	f[0], g[0] = 1, 1
	for i := 1; i < n; i++ {
		f[i] = g[i-1]
		g[i] = (f[i-1] + g[i-1]) % mod
	}
	v := f[n-1] + g[n-1]
	return v * v % mod
}

TypeScript

function countHousePlacements(n: number): number {
    const f = new Array(n);
    const g = new Array(n);
    f[0] = g[0] = 1n;
    const mod = BigInt(10 ** 9 + 7);
    for (let i = 1; i < n; ++i) {
        f[i] = g[i - 1];
        g[i] = (f[i - 1] + g[i - 1]) % mod;
    }
    const v = f[n - 1] + g[n - 1];
    return Number(v ** 2n % mod);
}

C#

public class Solution {
    public int CountHousePlacements(int n) {
        const int mod = (int) 1e9 + 7;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = g[0] = 1;
        for (int i = 1; i < n; ++i) {
            f[i] = g[i - 1];
            g[i] = (f[i - 1] + g[i - 1]) % mod;
        }
        long v = (f[n - 1] + g[n - 1]) % mod;
        return (int) (v * v % mod);
    }
}

...