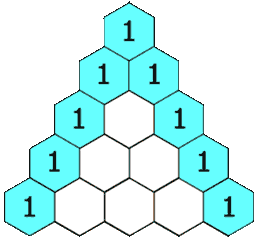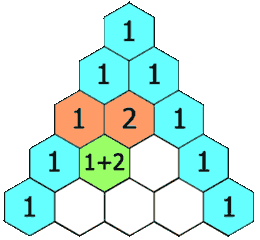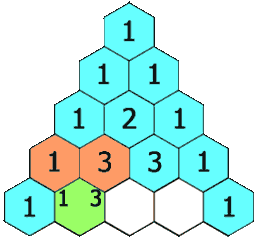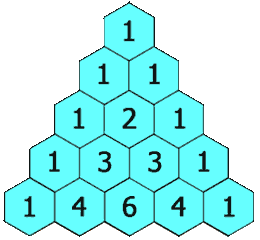
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
先设置每一行首尾元素为 1,其它元素为 0。然后根据杨辉三角,设置每一行其它元素即可。
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
res = []
for i in range(numRows):
t = [1 if j == 0 or j == i else 0 for j in range(i + 1)]
for j in range(1, i):
t[j] = res[i - 1][j - 1] + res[i - 1][j]
res.append(t)
return resclass Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < numRows; ++i) {
List<Integer> t = new ArrayList<>();
for (int j = 0; j < i + 1; ++j) {
boolean firstOrLast = j == 0 || j == i;
t.add(firstOrLast ? 1 : 0);
}
for (int j = 1; j < i; ++j) {
int val = res.get(i - 1).get(j - 1) + res.get(i - 1).get(j);
t.set(j, val);
}
res.add(t);
}
return res;
}
}function generate(numRows: number): number[][] {
if (numRows == 0) return [];
let ans = [[1]];
for (let i = 1; i < numRows; ++i) {
ans.push(new Array(i + 1).fill(1));
let half = i >> 1;
for (let j = 1; j <= half; ++j) {
let cur = ans[i - 1][j - 1] + ans[i - 1][j];
ans[i][j] = cur;
ans[i][i - j] = cur;
}
}
return ans;
}class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> res;
for (int i = 0; i < numRows; ++i) {
vector<int> t(i + 1);
t[0] = 1;
t[i] = 1;
for (int j = 1; j < i; ++j) {
t[j] = res[i - 1][j - 1] + res[i - 1][j];
}
res.push_back(t);
}
return res;
}
};func generate(numRows int) [][]int {
res := make([][]int, numRows)
for i := 0; i < numRows; i++ {
t := make([]int, i+1)
t[0] = 1
t[i] = 1
for j := 1; j < i; j++ {
t[j] = res[i-1][j-1] + res[i-1][j]
}
res[i] = t
}
return res
}const generate = function (numRows) {
let arr = [];
for (let i = 0; i < numRows; i++) {
let row = [];
row[0] = 1;
row[i] = 1;
for (let j = 1; j < row.length - 1; j++) {
row[j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
arr.push(row);
}
return arr;
};