README.md

comments	difficulty	edit_url	tags
true	困难	https://github.com/doocs/leetcode/edit/main/solution/0000-0099/0051.N-Queens/README.md	数组 回溯

51. N 皇后

English Version

题目描述

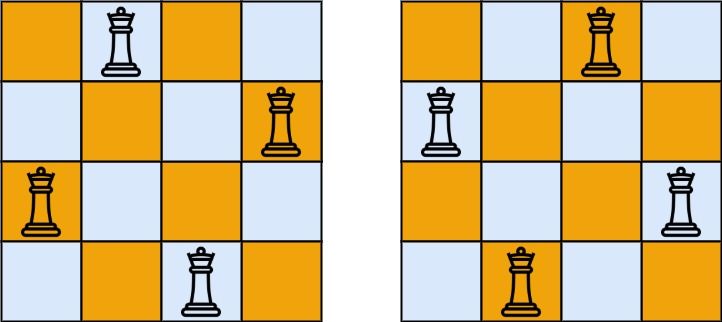
按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

 

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

 

提示：

• 1 <= n <= 9

解法

方法一：DFS(回溯)

我们定义三个数组 $col$, $dg$ 和 $udg$，分别表示列、正对角线和反对角线上的是否有皇后，如果位置 $(i, j)$ 有皇后，那么 $col[j]$, $dg[i + j]$ 和 $udg[n - i + j]$ 都为 $1$。另外，我们用一个数组 $g$ 记录当前棋盘的状态，初始时 $g$ 中的所有元素都是 '.'。

接下来，我们定义一个函数 $dfs(i)$，表示从第 $i$ 行开始放置皇后。

在 $dfs(i)$ 中，如果 $i=n$，说明我们已经完成了所有皇后的放置，我们将当前 $g$ 放入答案数组中，递归结束。

否则，我们枚举当前行的每一列 $j$，如果位置 $(i, j)$ 没有皇后，即 $col[j]$, $dg[i + j]$ 和 $udg[n - i + j]$ 都为 $0$，那么我们可以放置皇后，即把 $g[i][j]$ 改为 'Q'，并将 $col[j]$, $dg[i + j]$ 和 $udg[n - i + j]$ 都置为 $1$，然后继续搜索下一行，即调用 $dfs(i + 1)$，递归结束后，我们需要将 $g[i][j]$ 改回 '.' 并将 $col[j]$, $dg[i + j]$ 和 $udg[n - i + j]$ 都置为 $0$。

在主函数中，我们调用 $dfs(0)$ 开始递归，最后返回答案数组即可。

时间复杂度 $(n^2 \times n!)$，空间复杂度 $O(n)$。其中 $n$ 是题目给定的整数。

Python3

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        def dfs(i: int):
            if i == n:
                ans.append(["".join(row) for row in g])
                return
            for j in range(n):
                if col[j] + dg[i + j] + udg[n - i + j] == 0:
                    g[i][j] = "Q"
                    col[j] = dg[i + j] = udg[n - i + j] = 1
                    dfs(i + 1)
                    col[j] = dg[i + j] = udg[n - i + j] = 0
                    g[i][j] = "."

        ans = []
        g = [["."] * n for _ in range(n)]
        col = [0] * n
        dg = [0] * (n << 1)
        udg = [0] * (n << 1)
        dfs(0)
        return ans

Java

class Solution {
    private List<List<String>> ans = new ArrayList<>();
    private int[] col;
    private int[] dg;
    private int[] udg;
    private String[][] g;
    private int n;

    public List<List<String>> solveNQueens(int n) {
        this.n = n;
        col = new int[n];
        dg = new int[n << 1];
        udg = new int[n << 1];
        g = new String[n][n];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(g[i], ".");
        }
        dfs(0);
        return ans;
    }

    private void dfs(int i) {
        if (i == n) {
            List<String> t = new ArrayList<>();
            for (int j = 0; j < n; ++j) {
                t.add(String.join("", g[j]));
            }
            ans.add(t);
            return;
        }
        for (int j = 0; j < n; ++j) {
            if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
                g[i][j] = "Q";
                col[j] = dg[i + j] = udg[n - i + j] = 1;
                dfs(i + 1);
                col[j] = dg[i + j] = udg[n - i + j] = 0;
                g[i][j] = ".";
            }
        }
    }
}

C++

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<int> col(n);
        vector<int> dg(n << 1);
        vector<int> udg(n << 1);
        vector<vector<string>> ans;
        vector<string> t(n, string(n, '.'));
        function<void(int)> dfs = [&](int i) -> void {
            if (i == n) {
                ans.push_back(t);
                return;
            }
            for (int j = 0; j < n; ++j) {
                if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
                    t[i][j] = 'Q';
                    col[j] = dg[i + j] = udg[n - i + j] = 1;
                    dfs(i + 1);
                    col[j] = dg[i + j] = udg[n - i + j] = 0;
                    t[i][j] = '.';
                }
            }
        };
        dfs(0);
        return ans;
    }
};

Go

func solveNQueens(n int) (ans [][]string) {
	col := make([]int, n)
	dg := make([]int, n<<1)
	udg := make([]int, n<<1)
	t := make([][]byte, n)
	for i := range t {
		t[i] = make([]byte, n)
		for j := range t[i] {
			t[i][j] = '.'
		}
	}
	var dfs func(int)
	dfs = func(i int) {
		if i == n {
			tmp := make([]string, n)
			for i := range tmp {
				tmp[i] = string(t[i])
			}
			ans = append(ans, tmp)
			return
		}
		for j := 0; j < n; j++ {
			if col[j]+dg[i+j]+udg[n-i+j] == 0 {
				col[j], dg[i+j], udg[n-i+j] = 1, 1, 1
				t[i][j] = 'Q'
				dfs(i + 1)
				t[i][j] = '.'
				col[j], dg[i+j], udg[n-i+j] = 0, 0, 0
			}
		}
	}
	dfs(0)
	return
}

TypeScript

function solveNQueens(n: number): string[][] {
    const col: number[] = Array(n).fill(0);
    const dg: number[] = Array(n << 1).fill(0);
    const udg: number[] = Array(n << 1).fill(0);
    const ans: string[][] = [];
    const t: string[][] = Array.from({ length: n }, () => Array(n).fill('.'));
    const dfs = (i: number) => {
        if (i === n) {
            ans.push(t.map(x => x.join('')));
            return;
        }
        for (let j = 0; j < n; ++j) {
            if (col[j] + dg[i + j] + udg[n - i + j] === 0) {
                t[i][j] = 'Q';
                col[j] = dg[i + j] = udg[n - i + j] = 1;
                dfs(i + 1);
                col[j] = dg[i + j] = udg[n - i + j] = 0;
                t[i][j] = '.';
            }
        }
    };
    dfs(0);
    return ans;
}

C#

public class Solution {
    private int n;
    private int[] col;
    private int[] dg;
    private int[] udg;
    private IList<IList<string>> ans = new List<IList<string>>();
    private IList<string> t = new List<string>();

    public IList<IList<string>> SolveNQueens(int n) {
        this.n = n;
        col = new int[n];
        dg = new int[n << 1];
        udg = new int[n << 1];
        dfs(0);
        return ans;
    }

    private void dfs(int i) {
        if (i == n) {
            ans.Add(new List<string>(t));
            return;
        }
        for (int j = 0; j < n; ++j) {
            if (col[j] + dg[i + j] + udg[n - i + j] == 0) {
                char[] row = new char[n];
                Array.Fill(row, '.');
                row[j] = 'Q';
                t.Add(new string(row));
                col[j] = dg[i + j] = udg[n - i + j] = 1;
                dfs(i + 1);
                col[j] = dg[i + j] = udg[n - i + j] = 0;
                t.RemoveAt(t.Count - 1);
            }
        }
    }
}