Skip to content

Latest commit

 

History

History
300 lines (256 loc) · 8.25 KB

README.md

File metadata and controls

300 lines (256 loc) · 8.25 KB
Raw
comments difficulty edit_url tags
true
简单
树
二叉搜索树
数组
分治
二叉树

108. 将有序数组转换为二叉搜索树

English Version

题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

 

示例 1：

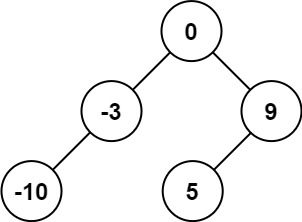
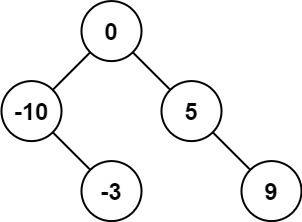
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：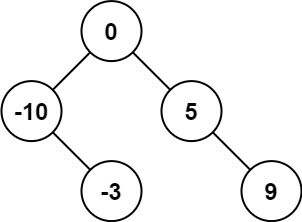

示例 2：

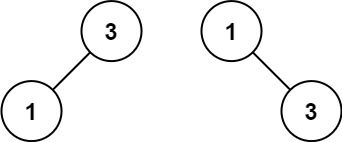
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

 

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

解法

方法一：二分 + 递归

我们设计一个递归函数 $dfs(l, r)$，表示当前待构造的二叉搜索树的节点值都在数组 nums 的下标范围 $[l, r]$ 内。该函数返回构造出的二叉搜索树的根节点。

函数 $dfs(l, r)$ 的执行流程如下：

  1. 如果 $l &gt; r$，说明当前数组为空，返回 null。
  2. 如果 $l \leq r$，取数组中下标为 $mid = \lfloor \frac{l + r}{2} \rfloor$ 的元素作为当前二叉搜索树的根节点，其中 $\lfloor x \rfloor$ 表示对 $x$ 向下取整。
  3. 递归地构造当前二叉搜索树的左子树，其根节点的值为数组中下标为 $mid - 1$ 的元素，左子树的节点值都在数组的下标范围 $[l, mid - 1]$ 内。
  4. 递归地构造当前二叉搜索树的右子树，其根节点的值为数组中下标为 $mid + 1$ 的元素，右子树的节点值都在数组的下标范围 $[mid + 1, r]$ 内。
  5. 返回当前二叉搜索树的根节点。

答案即为函数 $dfs(0, n - 1)$ 的返回值。

时间复杂度 $O(n)$，空间复杂度 $O(\log n)$。其中 $n$ 为数组 nums 的长度。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        def dfs(l, r):
            if l > r:
                return None
            mid = (l + r) >> 1
            left = dfs(l, mid - 1)
            right = dfs(mid + 1, r)
            return TreeNode(nums[mid], left, right)

        return dfs(0, len(nums) - 1)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] nums;

    public TreeNode sortedArrayToBST(int[] nums) {
        this.nums = nums;
        return dfs(0, nums.length - 1);
    }

    private TreeNode dfs(int l, int r) {
        if (l > r) {
            return null;
        }
        int mid = (l + r) >> 1;
        TreeNode left = dfs(l, mid - 1);
        TreeNode right = dfs(mid + 1, r);
        return new TreeNode(nums[mid], left, right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        function<TreeNode*(int, int)> dfs = [&](int l, int r) -> TreeNode* {
            if (l > r) {
                return nullptr;
            }
            int mid = (l + r) >> 1;
            auto left = dfs(l, mid - 1);
            auto right = dfs(mid + 1, r);
            return new TreeNode(nums[mid], left, right);
        };
        return dfs(0, nums.size() - 1);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sortedArrayToBST(nums []int) *TreeNode {
	var dfs func(int, int) *TreeNode
	dfs = func(l, r int) *TreeNode {
		if l > r {
			return nil
		}
		mid := (l + r) >> 1
		left, right := dfs(l, mid-1), dfs(mid+1, r)
		return &TreeNode{nums[mid], left, right}
	}
	return dfs(0, len(nums)-1)
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function sortedArrayToBST(nums: number[]): TreeNode | null {
    const n = nums.length;
    if (n === 0) {
        return null;
    }
    const mid = n >> 1;
    return new TreeNode(
        nums[mid],
        sortedArrayToBST(nums.slice(0, mid)),
        sortedArrayToBST(nums.slice(mid + 1)),
    );
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn to_bst(nums: &Vec<i32>, start: usize, end: usize) -> Option<Rc<RefCell<TreeNode>>> {
        if start >= end {
            return None;
        }
        let mid = start + (end - start) / 2;
        Some(Rc::new(RefCell::new(TreeNode {
            val: nums[mid],
            left: Self::to_bst(nums, start, mid),
            right: Self::to_bst(nums, mid + 1, end),
        })))
    }

    pub fn sorted_array_to_bst(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
        Self::to_bst(&nums, 0, nums.len())
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var sortedArrayToBST = function (nums) {
    const dfs = (l, r) => {
        if (l > r) {
            return null;
        }
        const mid = (l + r) >> 1;
        const left = dfs(l, mid - 1);
        const right = dfs(mid + 1, r);
        return new TreeNode(nums[mid], left, right);
    };
    return dfs(0, nums.length - 1);
};