Skip to content

Latest commit

 

History

History
247 lines (202 loc) · 5.9 KB

README.md

File metadata and controls

247 lines (202 loc) · 5.9 KB
Raw
comments difficulty edit_url tags
true
中等
树
深度优先搜索
二叉搜索树
二叉树

285. 二叉搜索树中的中序后继 🔒

English Version

题目描述

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点 p 的后继是值比 p.val 大的节点中键值最小的节点。

 

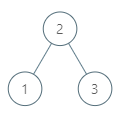
示例 1：

输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。

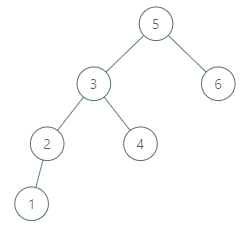
示例 2：

输入：root = [5,3,6,2,4,null,null,1], p = 6
输出：null
解释：因为给出的节点没有中序后继，所以答案就返回 null 了。

 

提示：

  • 树中节点的数目在范围 [1, 104] 内。
  • -105 <= Node.val <= 105
  • 树中各节点的值均保证唯一。

解法

方法一：二分搜索

二叉搜索树的中序遍历是一个升序序列，因此可以使用二分搜索的方法。

二叉搜索树节点 $p$ 的中序后继节点满足：

  1. 中序后继的节点值大于 $p$ 的节点值
  2. 中序后继是所有大于 $p$ 的节点中值最小的节点

因此，对于当前节点 $root$，如果 $root.val \gt p.val$，则 $root$ 可能是 $p$ 的中序后继节点，将 $root$ 记为 $ans$，然后搜索左子树，即 $root = root.left$；如果 $root.val \leq p.val$，则 $root$ 不能是 $p$ 的中序后继节点，搜索右子树，即 $root = root.right$。

时间复杂度 $O(h)$，其中 $h$ 为二叉搜索树的高度。空间复杂度 $O(1)$。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def inorderSuccessor(self, root: TreeNode, p: TreeNode) -> Optional[TreeNode]:
        ans = None
        while root:
            if root.val > p.val:
                ans = root
                root = root.left
            else:
                root = root.right
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        TreeNode ans = null;
        while (root != null) {
            if (root.val > p.val) {
                ans = root;
                root = root.left;
            } else {
                root = root.right;
            }
        }
        return ans;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode* ans = nullptr;
        while (root) {
            if (root->val > p->val) {
                ans = root;
                root = root->left;
            } else {
                root = root->right;
            }
        }
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func inorderSuccessor(root *TreeNode, p *TreeNode) (ans *TreeNode) {
	for root != nil {
		if root.Val > p.Val {
			ans = root
			root = root.Left
		} else {
			root = root.Right
		}
	}
	return
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function inorderSuccessor(root: TreeNode | null, p: TreeNode | null): TreeNode | null {
    let ans: TreeNode | null = null;
    while (root) {
        if (root.val > p.val) {
            ans = root;
            root = root.left;
        } else {
            root = root.right;
        }
    }
    return ans;
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @return {TreeNode}
 */
var inorderSuccessor = function (root, p) {
    let ans = null;
    while (root) {
        if (root.val > p.val) {
            ans = root;
            root = root.left;
        } else {
            root = root.right;
        }
    }
    return ans;
};