README.md

comments	difficulty	edit_url	tags
true	困难	https://github.com/doocs/leetcode/edit/main/solution/0300-0399/0335.Self%20Crossing/README.md	几何 数组 数学

335. 路径交叉

English Version

题目描述

给你一个整数数组 distance 。

从 X-Y 平面上的点 (0,0) 开始，先向北移动 distance[0] 米，然后向西移动 distance[1] 米，向南移动 distance[2] 米，向东移动 distance[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

判断你所经过的路径是否相交。如果相交，返回 true ；否则，返回 false 。

 

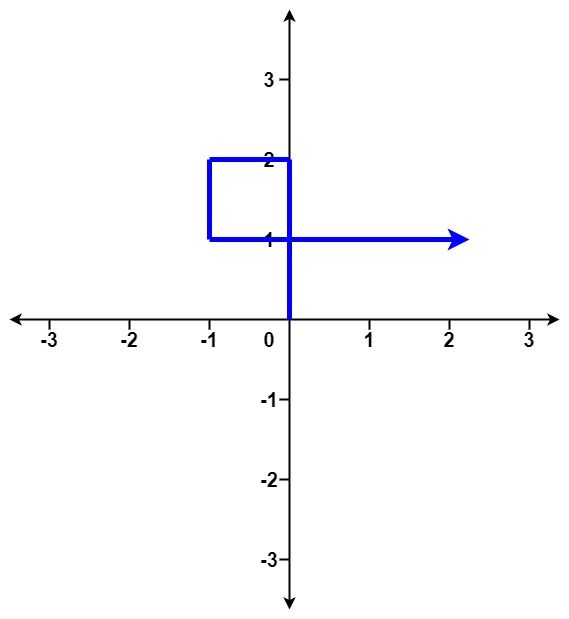
示例 1：

输入：distance = [2,1,1,2]
输出：true

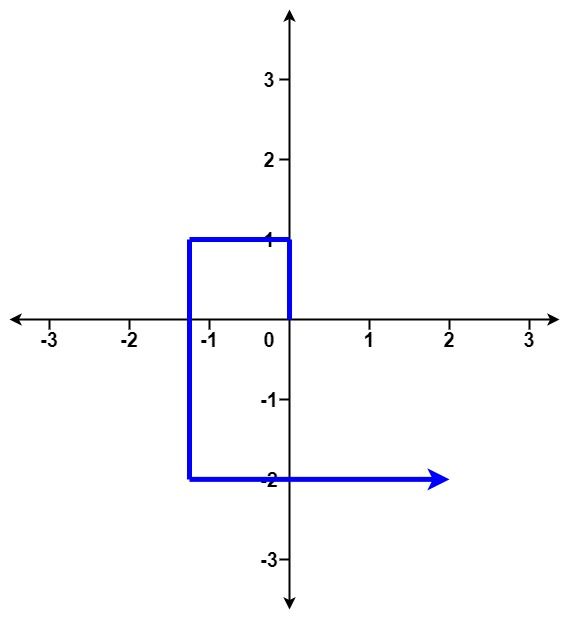
示例 2：

输入：distance = [1,2,3,4]
输出：false

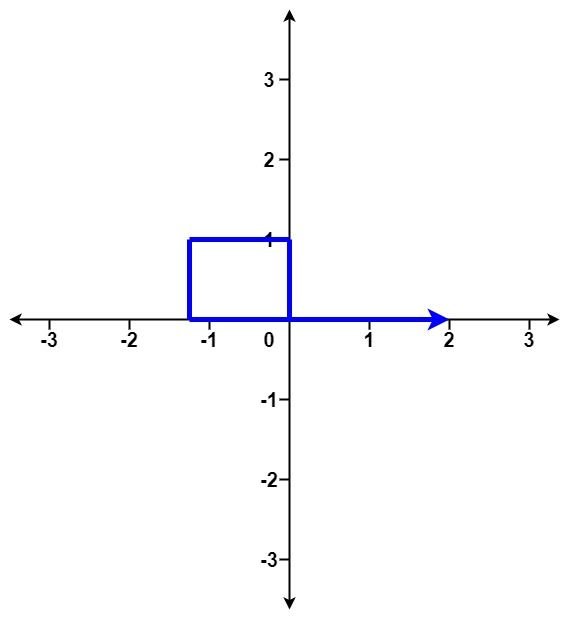
示例 3：

输入：distance = [1,1,1,1]
输出：true

 

提示：

• 1 <= distance.length <= 105
• 1 <= distance[i] <= 105

解法

方法一

Python3

class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        d = distance
        for i in range(3, len(d)):
            if d[i] >= d[i - 2] and d[i - 1] <= d[i - 3]:
                return True
            if i >= 4 and d[i - 1] == d[i - 3] and d[i] + d[i - 4] >= d[i - 2]:
                return True
            if (
                i >= 5
                and d[i - 2] >= d[i - 4]
                and d[i - 1] <= d[i - 3]
                and d[i] >= d[i - 2] - d[i - 4]
                and d[i - 1] + d[i - 5] >= d[i - 3]
            ):
                return True
        return False

Java

class Solution {
    public boolean isSelfCrossing(int[] distance) {
        int[] d = distance;
        for (int i = 3; i < d.length; ++i) {
            if (d[i] >= d[i - 2] && d[i - 1] <= d[i - 3]) {
                return true;
            }
            if (i >= 4 && d[i - 1] == d[i - 3] && d[i] + d[i - 4] >= d[i - 2]) {
                return true;
            }
            if (i >= 5 && d[i - 2] >= d[i - 4] && d[i - 1] <= d[i - 3]
                && d[i] >= d[i - 2] - d[i - 4] && d[i - 1] + d[i - 5] >= d[i - 3]) {
                return true;
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool isSelfCrossing(vector<int>& distance) {
        vector<int> d = distance;
        for (int i = 3; i < d.size(); ++i) {
            if (d[i] >= d[i - 2] && d[i - 1] <= d[i - 3]) return true;
            if (i >= 4 && d[i - 1] == d[i - 3] && d[i] + d[i - 4] >= d[i - 2]) return true;
            if (i >= 5 && d[i - 2] >= d[i - 4] && d[i - 1] <= d[i - 3] && d[i] >= d[i - 2] - d[i - 4] && d[i - 1] + d[i - 5] >= d[i - 3]) return true;
        }
        return false;
    }
};

Go

func isSelfCrossing(distance []int) bool {
	d := distance
	for i := 3; i < len(d); i++ {
		if d[i] >= d[i-2] && d[i-1] <= d[i-3] {
			return true
		}
		if i >= 4 && d[i-1] == d[i-3] && d[i]+d[i-4] >= d[i-2] {
			return true
		}
		if i >= 5 && d[i-2] >= d[i-4] && d[i-1] <= d[i-3] && d[i] >= d[i-2]-d[i-4] && d[i-1]+d[i-5] >= d[i-3] {
			return true
		}
	}
	return false
}

C#

public class Solution {
    public bool IsSelfCrossing(int[] x) {
        for (var i = 3; i < x.Length; ++i)
        {
            if (x[i] >= x[i - 2] && x[i - 1] <= x[i - 3]) return true;
            if (i > 3 && x[i] + x[i - 4] >= x[i - 2])
            {
                if (x[i - 1] == x[i - 3]) return true;
                if (i > 4 && x[i - 2] >= x[i - 4] && x[i - 1] <= x[i - 3] && x[i - 1] + x[i - 5] >= x[i - 3]) return true;
            }
        }
        return false;
    }
}