README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0300-0399/0351.Android%20Unlock%20Patterns/README.md	位运算 动态规划 回溯 状态压缩

351. 安卓系统手势解锁 🔒

English Version

题目描述

我们都知道安卓有个手势解锁的界面，是一个 3 x 3 的点所绘制出来的网格。用户可以设置一个 “解锁模式” ，通过连接特定序列中的点，形成一系列彼此连接的线段，每个线段的端点都是序列中两个连续的点。如果满足以下两个条件，则 k 点序列是有效的解锁模式：

• 解锁模式中的所有点 互不相同 。
• 假如模式中两个连续点的线段需要经过其他点的 中心 ，那么要经过的点 必须提前出现 在序列中（已经经过），不能跨过任何还未被经过的点。
  • 例如，点 5 或 6 没有提前出现的情况下连接点 2 和 9 是有效的，因为从点 2 到点 9 的线没有穿过点 5 或 6 的中心。
  • 然而，点 2 没有提前出现的情况下连接点 1 和 3 是无效的，因为从圆点 1 到圆点 3 的直线穿过圆点 2 的中心。

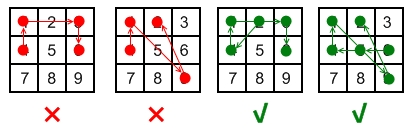
以下是一些有效和无效解锁模式的示例：

• 无效手势：[4,1,3,6] ，连接点 1 和点 3 时经过了未被连接过的 2 号点。
• 无效手势：[4,1,9,2] ，连接点 1 和点 9 时经过了未被连接过的 5 号点。
• 有效手势：[2,4,1,3,6] ，连接点 1 和点 3 是有效的，因为虽然它经过了点 2 ，但是点 2 在该手势中之前已经被连过了。
• 有效手势：[6,5,4,1,9,2] ，连接点 1 和点 9 是有效的，因为虽然它经过了按键 5 ，但是点 5 在该手势中之前已经被连过了。

给你两个整数，分别为 ​​m 和 n ，那么请返回有多少种 不同且有效的解锁模式 ，是 至少 需要经过 m 个点，但是 不超过 n 个点的。

两个解锁模式 不同 需满足：经过的点不同或者经过点的顺序不同。

 

示例 1：

输入：m = 1, n = 1
输出：9

示例 2：

输入：m = 1, n = 2
输出：65

 

提示：

• 1 <= m, n <= 9

解法

方法一：DFS

我们定义一个二维数组 $cross$，其中 $cross[i][j]$ 表示数字 $i$ 和数字 $j$ 之间是否有中间数字，如果有则 $cross[i][j]$ 的值为中间数字，否则为 $0$。

我们还需要一个一维数组 $vis$，用来记录数字是否被使用过。

由于数字 $1$, $3$, $7$, $9$ 是对称的，因此我们只需要计算数字 $1$ 的情况，然后乘以 $4$ 即可。

由于数字 $2$, $4$, $6$, $8$ 也是对称的，因此我们只需要计算数字 $2$ 的情况，然后乘以 $4$ 即可。

最后我们再计算数字 $5$ 的情况。

我们设计一个函数 $dfs(i, cnt)$，表示当前位于数字 $i$，且已经选了 $cnt$ 个数字的情况下，有多少种解锁模式。

函数 $dfs(i, cnt)$ 的执行过程如下：

如果 $cnt \gt n$，说明当前选中的数字个数超过了 $n$，直接返回 $0$。

否则，我们将数字 $i$ 标记为已使用，然后初始化答案 $ans$ 为 $0$。如果 $cnt \ge m$，说明当前选中的数字个数不少于 $m$，那么答案 $ans$ 就需要加 $1$。

接下来，我们枚举下一个数字 $j$，如果数字 $j$ 没有被使用过，且数字 $i$ 和数字 $j$ 之间没有中间数字，或者数字 $i$ 和数字 $j$ 之间的中间数字已经被使用过，那么我们就可以从数字 $j$ 出发，继续搜索，此时答案 $ans$ 需要加上 $dfs(j, cnt + 1)$ 的返回值。

最后，我们将数字 $i$ 标记为未使用，然后返回答案 $ans$。

最终的答案即为 $dfs(1, 1) \times 4 + dfs(2, 1) \times 4 + dfs(5, 1)$。

时间复杂度 $O(n!)$，空间复杂度 $O(n)$。其中 $n$ 是手势的最大长度。

Python3

class Solution:
    def numberOfPatterns(self, m: int, n: int) -> int:
        def dfs(i: int, cnt: int = 1) -> int:
            if cnt > n:
                return 0
            vis[i] = True
            ans = int(cnt >= m)
            for j in range(1, 10):
                x = cross[i][j]
                if not vis[j] and (x == 0 or vis[x]):
                    ans += dfs(j, cnt + 1)
            vis[i] = False
            return ans

        cross = [[0] * 10 for _ in range(10)]
        cross[1][3] = cross[3][1] = 2
        cross[1][7] = cross[7][1] = 4
        cross[1][9] = cross[9][1] = 5
        cross[2][8] = cross[8][2] = 5
        cross[3][7] = cross[7][3] = 5
        cross[3][9] = cross[9][3] = 6
        cross[4][6] = cross[6][4] = 5
        cross[7][9] = cross[9][7] = 8
        vis = [False] * 10
        return dfs(1) * 4 + dfs(2) * 4 + dfs(5)

Java

class Solution {
    private int m;
    private int n;
    private int[][] cross = new int[10][10];
    private boolean[] vis = new boolean[10];

    public int numberOfPatterns(int m, int n) {
        this.m = m;
        this.n = n;
        cross[1][3] = cross[3][1] = 2;
        cross[1][7] = cross[7][1] = 4;
        cross[1][9] = cross[9][1] = 5;
        cross[2][8] = cross[8][2] = 5;
        cross[3][7] = cross[7][3] = 5;
        cross[3][9] = cross[9][3] = 6;
        cross[4][6] = cross[6][4] = 5;
        cross[7][9] = cross[9][7] = 8;
        return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
    }

    private int dfs(int i, int cnt) {
        if (cnt > n) {
            return 0;
        }
        vis[i] = true;
        int ans = cnt >= m ? 1 : 0;
        for (int j = 1; j < 10; ++j) {
            int x = cross[i][j];
            if (!vis[j] && (x == 0 || vis[x])) {
                ans += dfs(j, cnt + 1);
            }
        }
        vis[i] = false;
        return ans;
    }
}

C++

class Solution {
public:
    int numberOfPatterns(int m, int n) {
        int cross[10][10];
        memset(cross, 0, sizeof(cross));
        bool vis[10];
        memset(vis, false, sizeof(vis));
        cross[1][3] = cross[3][1] = 2;
        cross[1][7] = cross[7][1] = 4;
        cross[1][9] = cross[9][1] = 5;
        cross[2][8] = cross[8][2] = 5;
        cross[3][7] = cross[7][3] = 5;
        cross[3][9] = cross[9][3] = 6;
        cross[4][6] = cross[6][4] = 5;
        cross[7][9] = cross[9][7] = 8;

        function<int(int, int)> dfs = [&](int i, int cnt) {
            if (cnt > n) {
                return 0;
            }
            vis[i] = true;
            int ans = cnt >= m ? 1 : 0;
            for (int j = 1; j < 10; ++j) {
                int x = cross[i][j];
                if (!vis[j] && (x == 0 || vis[x])) {
                    ans += dfs(j, cnt + 1);
                }
            }
            vis[i] = false;
            return ans;
        };

        return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
    }
};

Go

func numberOfPatterns(m int, n int) int {
	cross := [10][10]int{}
	vis := [10]bool{}
	cross[1][3] = 2
	cross[1][7] = 4
	cross[1][9] = 5
	cross[2][8] = 5
	cross[3][7] = 5
	cross[3][9] = 6
	cross[4][6] = 5
	cross[7][9] = 8
	cross[3][1] = 2
	cross[7][1] = 4
	cross[9][1] = 5
	cross[8][2] = 5
	cross[7][3] = 5
	cross[9][3] = 6
	cross[6][4] = 5
	cross[9][7] = 8
	var dfs func(int, int) int
	dfs = func(i, cnt int) int {
		if cnt > n {
			return 0
		}
		vis[i] = true
		ans := 0
		if cnt >= m {
			ans++
		}
		for j := 1; j < 10; j++ {
			x := cross[i][j]
			if !vis[j] && (x == 0 || vis[x]) {
				ans += dfs(j, cnt+1)
			}
		}
		vis[i] = false
		return ans
	}
	return dfs(1, 1)*4 + dfs(2, 1)*4 + dfs(5, 1)
}

TypeScript

function numberOfPatterns(m: number, n: number): number {
    const cross: number[][] = Array(10)
        .fill(0)
        .map(() => Array(10).fill(0));
    const vis: boolean[] = Array(10).fill(false);
    cross[1][3] = cross[3][1] = 2;
    cross[1][7] = cross[7][1] = 4;
    cross[1][9] = cross[9][1] = 5;
    cross[2][8] = cross[8][2] = 5;
    cross[3][7] = cross[7][3] = 5;
    cross[3][9] = cross[9][3] = 6;
    cross[4][6] = cross[6][4] = 5;
    cross[7][9] = cross[9][7] = 8;
    const dfs = (i: number, cnt: number): number => {
        if (cnt > n) {
            return 0;
        }
        vis[i] = true;
        let ans = 0;
        if (cnt >= m) {
            ++ans;
        }
        for (let j = 1; j < 10; ++j) {
            const x = cross[i][j];
            if (!vis[j] && (x === 0 || vis[x])) {
                ans += dfs(j, cnt + 1);
            }
        }
        vis[i] = false;
        return ans;
    };
    return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
}