| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
true |
困难 |
|
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
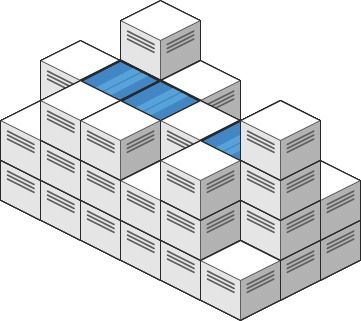
示例 1:
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 输出: 4 解释: 下雨后,雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。
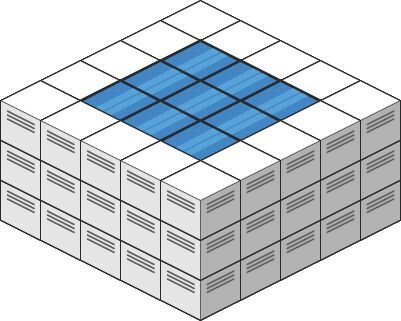
示例 2:
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]] 输出: 10
提示:
m == heightMap.lengthn == heightMap[i].length1 <= m, n <= 2000 <= heightMap[i][j] <= 2 * 104
接雨水问题的变种,由于矩阵的边界上的高度是确定的,因此可以将矩阵的边界上的高度加入优先队列,然后从优先队列中取出最小的高度,然后将其四周的高度与其比较,如果四周的高度小于当前高度,则可以接雨水,接雨水的体积为当前高度减去四周的高度,然后将较大的高度加入优先队列,重复上述过程,直到优先队列为空。
时间复杂度
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
m, n = len(heightMap), len(heightMap[0])
vis = [[False] * n for _ in range(m)]
pq = []
for i in range(m):
for j in range(n):
if i == 0 or i == m - 1 or j == 0 or j == n - 1:
heappush(pq, (heightMap[i][j], i, j))
vis[i][j] = True
ans = 0
dirs = (-1, 0, 1, 0, -1)
while pq:
h, i, j = heappop(pq)
for a, b in pairwise(dirs):
x, y = i + a, j + b
if x >= 0 and x < m and y >= 0 and y < n and not vis[x][y]:
ans += max(0, h - heightMap[x][y])
vis[x][y] = True
heappush(pq, (max(h, heightMap[x][y]), x, y))
return ansclass Solution {
public int trapRainWater(int[][] heightMap) {
int m = heightMap.length, n = heightMap[0].length;
boolean[][] vis = new boolean[m][n];
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
pq.offer(new int[] {heightMap[i][j], i, j});
vis[i][j] = true;
}
}
}
int ans = 0;
int[] dirs = {-1, 0, 1, 0, -1};
while (!pq.isEmpty()) {
var p = pq.poll();
for (int k = 0; k < 4; ++k) {
int x = p[1] + dirs[k], y = p[2] + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
ans += Math.max(0, p[0] - heightMap[x][y]);
vis[x][y] = true;
pq.offer(new int[] {Math.max(p[0], heightMap[x][y]), x, y});
}
}
}
return ans;
}
}class Solution {
public:
int trapRainWater(vector<vector<int>>& heightMap) {
using tii = tuple<int, int, int>;
priority_queue<tii, vector<tii>, greater<tii>> pq;
int m = heightMap.size(), n = heightMap[0].size();
bool vis[m][n];
memset(vis, 0, sizeof vis);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
pq.emplace(heightMap[i][j], i, j);
vis[i][j] = true;
}
}
}
int ans = 0;
int dirs[5] = {-1, 0, 1, 0, -1};
while (!pq.empty()) {
auto [h, i, j] = pq.top();
pq.pop();
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]) {
ans += max(0, h - heightMap[x][y]);
vis[x][y] = true;
pq.emplace(max(heightMap[x][y], h), x, y);
}
}
}
return ans;
}
};func trapRainWater(heightMap [][]int) (ans int) {
m, n := len(heightMap), len(heightMap[0])
pq := hp{}
vis := make([][]bool, m)
for i, row := range heightMap {
vis[i] = make([]bool, n)
for j, v := range row {
if i == 0 || i == m-1 || j == 0 || j == n-1 {
heap.Push(&pq, tuple{v, i, j})
vis[i][j] = true
}
}
}
dirs := []int{-1, 0, 1, 0, -1}
for len(pq) > 0 {
p := heap.Pop(&pq).(tuple)
for k := 0; k < 4; k++ {
x, y := p.i+dirs[k], p.j+dirs[k+1]
if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] {
ans += max(0, p.v-heightMap[x][y])
vis[x][y] = true
heap.Push(&pq, tuple{max(p.v, heightMap[x][y]), x, y})
}
}
}
return
}
type tuple struct{ v, i, j int }
type hp []tuple
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].v < h[j].v }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any) { *h = append(*h, v.(tuple)) }
func (h *hp) Pop() any { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }