comments

difficulty

edit_url

431. 将 N 叉树编码为二叉树 🔒

题目描述

设计一个算法，可以将 N 叉树编码为二叉树，并能将该二叉树解码为原 N 叉树。一个 N 叉树是指每个节点都有不超过 N 个孩子节点的有根树。类似地，一个二叉树是指每个节点都有不超过 2 个孩子节点的有根树。你的编码 / 解码的算法的实现没有限制，你只需要保证一个 N 叉树可以编码为二叉树且该二叉树可以解码回原始 N 叉树即可。

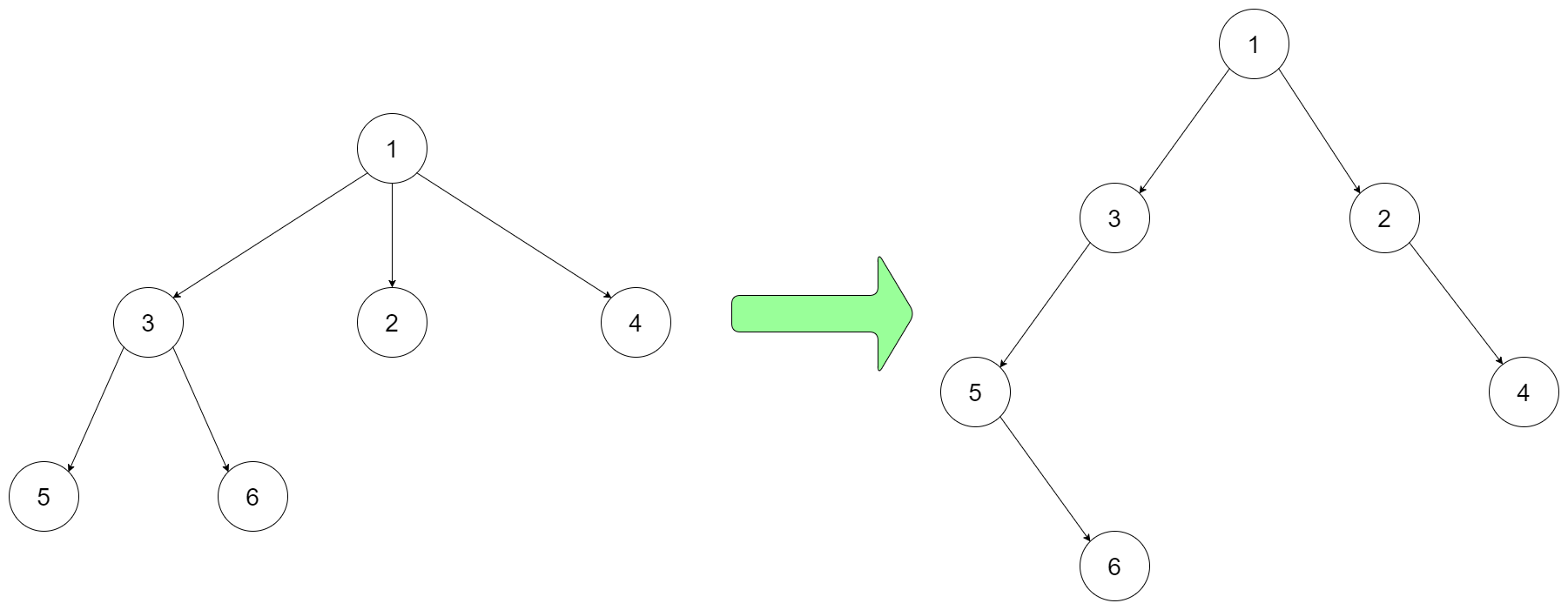
例如，你可以将下面的 3-叉 树以该种方式编码：

输入：root = [1,null,3,2,4,null,5,6]

注意，上面的方法仅仅是一个例子，可能可行也可能不可行。你没有必要遵循这种形式转化，你可以自己创造和实现不同的方法。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[1,null,3,2,4,null,5,6]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

示例 3：

输入：root = []
输出：[]

提示：

N 的范围在 [1, 10⁴]
0 <= Node.val <= 10⁴
N 叉树的高度小于等于 1000。
不要使用类成员 / 全局变量 / 静态变量来存储状态。你的编码和解码算法应是无状态的。

解法

方法一：递归

我们可以将二叉树的左指针指向 N 叉树的第一个孩子，将二叉树的右指针指向 N 叉树的下一个兄弟节点。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为 N 叉树的节点数量。

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""

"""
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
"""


class Codec:
    # Encodes an n-ary tree to a binary tree.
    def encode(self, root: "Optional[Node]") -> Optional[TreeNode]:
        if root is None:
            return None
        node = TreeNode(root.val)
        if not root.children:
            return node
        left = self.encode(root.children[0])
        node.left = left
        for child in root.children[1:]:
            left.right = self.encode(child)
            left = left.right
        return node

    # Decodes your binary tree to an n-ary tree.
    def decode(self, data: Optional[TreeNode]) -> "Optional[Node]":
        if data is None:
            return None
        node = Node(data.val, [])
        if data.left is None:
            return node
        left = data.left
        while left:
            node.children.append(self.decode(left))
            left = left.right
        return node


# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.decode(codec.encode(root))

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Codec {
    // Encodes an n-ary tree to a binary tree.
    public TreeNode encode(Node root) {
        if (root == null) {
            return null;
        }
        TreeNode node = new TreeNode(root.val);
        if (root.children == null || root.children.isEmpty()) {
            return node;
        }
        TreeNode left = encode(root.children.get(0));
        node.left = left;
        for (int i = 1; i < root.children.size(); i++) {
            left.right = encode(root.children.get(i));
            left = left.right;
        }
        return node;
    }

    // Decodes your binary tree to an n-ary tree.
    public Node decode(TreeNode data) {
        if (data == null) {
            return null;
        }
        Node node = new Node(data.val, new ArrayList<>());
        if (data.left == null) {
            return node;
        }
        TreeNode left = data.left;
        while (left != null) {
            node.children.add(decode(left));
            left = left.right;
        }
        return node;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.decode(codec.encode(root));

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Codec {
public:
    // Encodes an n-ary tree to a binary tree.
    TreeNode* encode(Node* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* node = new TreeNode(root->val);
        if (root->children.empty()) {
            return node;
        }
        TreeNode* left = encode(root->children[0]);
        node->left = left;
        for (int i = 1; i < root->children.size(); i++) {
            left->right = encode(root->children[i]);
            left = left->right;
        }
        return node;
    }

    // Decodes your binary tree to an n-ary tree.
    Node* decode(TreeNode* data) {
        if (data == nullptr) {
            return nullptr;
        }
        Node* node = new Node(data->val, vector<Node*>());
        if (data->left == nullptr) {
            return node;
        }
        TreeNode* left = data->left;
        while (left != nullptr) {
            node->children.push_back(decode(left));
            left = left->right;
        }
        return node;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.decode(codec.encode(root));

Go

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

type Codec struct {
}

func Constructor() *Codec {
	return &Codec{}
}

// Encodes an n-ary tree to a binary tree.
func (this *Codec) encode(root *Node) *TreeNode {
	if root == nil {
		return nil
	}
	node := &TreeNode{Val: root.Val}
	if len(root.Children) == 0 {
		return node
	}
	left := this.encode(root.Children[0])
	node.Left = left
	for i := 1; i < len(root.Children); i++ {
		left.Right = this.encode(root.Children[i])
		left = left.Right
	}
	return node
}

// Decodes your binary tree to an n-ary tree.
func (this *Codec) decode(data *TreeNode) *Node {
	if data == nil {
		return nil
	}
	node := &Node{Val: data.Val, Children: []*Node{}}
	if data.Left == nil {
		return node
	}
	left := data.Left
	for left != nil {
		node.Children = append(node.Children, this.decode(left))
		left = left.Right
	}
	return node
}

/**
 * Your Codec object will be instantiated and called as such:
 * obj := Constructor();
 * bst := obj.encode(root);
 * ans := obj.decode(bst);
 */

TypeScript

/**
 * Definition for _Node.
 * class _Node {
 *     val: number
 *     children: _Node[]
 *
 *     constructor(v: number) {
 *         this.val = v;
 *         this.children = [];
 *     }
 * }
 */

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

class Codec {
    constructor() {}

    // Encodes an n-ary tree to a binary tree.
    serialize(root: _Node | null): TreeNode | null {
        if (root === null) {
            return null;
        }
        const node = new TreeNode(root.val);
        if (root.children.length === 0) {
            return node;
        }
        let left: TreeNode | null = this.serialize(root.children[0]);
        node.left = left;
        for (let i = 1; i < root.children.length; i++) {
            if (left) {
                left.right = this.serialize(root.children[i]);
                left = left.right;
            }
        }
        return node;
    }

    // Decodes your binary tree back to an n-ary tree.
    deserialize(root: TreeNode | null): _Node | null {
        if (root === null) {
            return null;
        }
        const node = new _Node(root.val);
        if (root.left === null) {
            return node;
        }
        let left: TreeNode | null = root.left;
        while (left !== null) {
            node.children.push(this.deserialize(left));
            left = left.right;
        }
        return node;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

431. 将 N 叉树编码为二叉树 🔒

题目描述

解法

方法一：递归

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

431. 将 N 叉树编码为二叉树 🔒

题目描述

解法

方法一：递归

Python3

Java

C++

Go

TypeScript