Skip to content

Latest commit

 

History

History
258 lines (210 loc) · 6.84 KB

README.md

File metadata and controls

258 lines (210 loc) · 6.84 KB
Raw
comments difficulty edit_url tags
true
简单
数组
矩阵
模拟

566. 重塑矩阵

English Version

题目描述

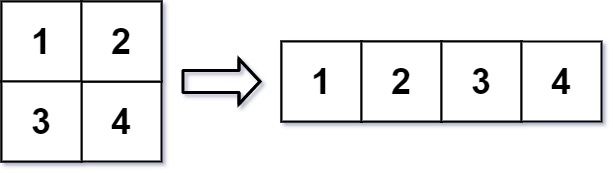
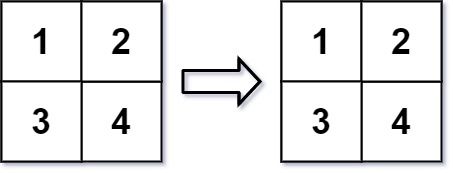
在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。

给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。

如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

 

示例 1：

输入：mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]

示例 2：

输入：mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

 

提示：

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • -1000 <= mat[i][j] <= 1000
  • 1 <= r, c <= 300

解法

方法一：模拟

我们先获取原矩阵的行数和列数，分别记为 $m$ 和 $n$。如果 $m \times n \neq r \times c$，则无法重塑矩阵，直接返回原矩阵。

否则，我们创建一个新矩阵，新矩阵的行数为 $r$，列数为 $c$。我们从原矩阵的第一个元素开始，按照行优先的顺序遍历原矩阵的所有元素，将遍历到的元素按顺序放入新矩阵中。

遍历完原矩阵的所有元素后，我们即可得到答案。

时间复杂度 $O(m \times n)$，其中 $m$ 和 $n$ 分别是原矩阵的行数和列数。忽略答案的空间消耗，空间复杂度 $O(1)$。

Python3

class Solution:
    def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        if m * n != r * c:
            return mat
        ans = [[0] * c for _ in range(r)]
        for i in range(m * n):
            ans[i // c][i % c] = mat[i // n][i % n]
        return ans

Java

class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length, n = mat[0].length;
        if (m * n != r * c) {
            return mat;
        }
        int[][] ans = new int[r][c];
        for (int i = 0; i < m * n; ++i) {
            ans[i / c][i % c] = mat[i / n][i % n];
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int m = mat.size(), n = mat[0].size();
        if (m * n != r * c) {
            return mat;
        }
        vector<vector<int>> ans(r, vector<int>(c));
        for (int i = 0; i < m * n; ++i) {
            ans[i / c][i % c] = mat[i / n][i % n];
        }
        return ans;
    }
};

Go

func matrixReshape(mat [][]int, r int, c int) [][]int {
	m, n := len(mat), len(mat[0])
	if m*n != r*c {
		return mat
	}
	ans := make([][]int, r)
	for i := range ans {
		ans[i] = make([]int, c)
	}
	for i := 0; i < m*n; i++ {
		ans[i/c][i%c] = mat[i/n][i%n]
	}
	return ans
}

TypeScript

function matrixReshape(mat: number[][], r: number, c: number): number[][] {
    let m = mat.length,
        n = mat[0].length;
    if (m * n != r * c) return mat;
    let ans = Array.from({ length: r }, v => new Array(c).fill(0));
    let k = 0;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            ans[Math.floor(k / c)][k % c] = mat[i][j];
            ++k;
        }
    }
    return ans;
}

Rust

impl Solution {
    pub fn matrix_reshape(mat: Vec<Vec<i32>>, r: i32, c: i32) -> Vec<Vec<i32>> {
        let r = r as usize;
        let c = c as usize;
        let m = mat.len();
        let n = mat[0].len();
        if m * n != r * c {
            return mat;
        }
        let mut i = 0;
        let mut j = 0;
        (0..r)
            .into_iter()
            .map(|_| {
                (0..c)
                    .into_iter()
                    .map(|_| {
                        let res = mat[i][j];
                        j += 1;
                        if j == n {
                            j = 0;
                            i += 1;
                        }
                        res
                    })
                    .collect()
            })
            .collect()
    }
}

C

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** matrixReshape(int** mat, int matSize, int* matColSize, int r, int c, int* returnSize, int** returnColumnSizes) {
    if (matSize * matColSize[0] != r * c) {
        *returnSize = matSize;
        *returnColumnSizes = matColSize;
        return mat;
    }
    *returnSize = r;
    *returnColumnSizes = malloc(sizeof(int) * r);
    int** ans = malloc(sizeof(int*) * r);
    for (int i = 0; i < r; i++) {
        (*returnColumnSizes)[i] = c;
        ans[i] = malloc(sizeof(int) * c);
    }
    for (int i = 0; i < r * c; i++) {
        ans[i / c][i % c] = mat[i / matColSize[0]][i % matColSize[0]];
    }
    return ans;
}

方法二

TypeScript

function matrixReshape(mat: number[][], r: number, c: number): number[][] {
    const m = mat.length;
    const n = mat[0].length;
    if (m * n !== r * c) {
        return mat;
    }
    const ans = Array.from({ length: r }, () => new Array(c).fill(0));
    for (let i = 0; i < r * c; i++) {
        ans[Math.floor(i / c)][i % c] = mat[Math.floor(i / n)][i % n];
    }
    return ans;
}