Skip to content

Latest commit

 

History

History
187 lines (149 loc) · 5.36 KB

README.md

File metadata and controls

187 lines (149 loc) · 5.36 KB
Raw
comments difficulty edit_url tags
true
中等
数组
数学

573. 松鼠模拟 🔒

English Version

题目描述

给你两个整数 height 和 width ，代表一个大小为 height x width 的花园。你还得到了以下信息：

  • 一个数组 tree ，其中 tree = [treer, treec] 是花园中树的位置，
  • 一个数组 squirrel ，其中 squirrel = [squirrelr, squirrelc] 是花园中松鼠的位置，
  • 一个数组 nuts ，其中 nuts[i] = [nutir, nutic] 是花园中第 ith 个坚果的位置。

松鼠一次最多只能携带一个坚果，并且能够向上、下、左、右四个方向移动到相邻的单元格。

返回松鼠收集所有坚果并逐一放在树下的 最小距离 。

距离 是指移动的次数。

 

示例 1：

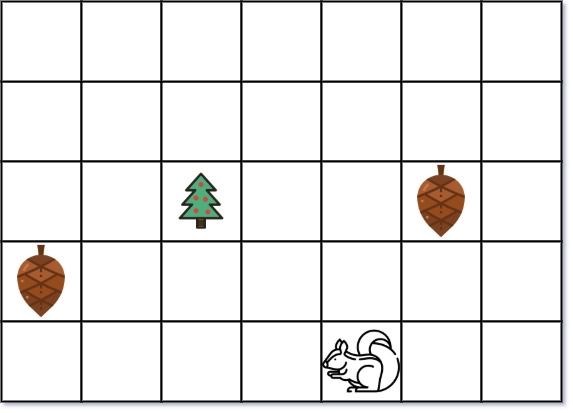
输入：height = 5, width = 7, tree = [2,2], squirrel = [4,4], nuts = [[3,0], [2,5]]
输出：12
解释：为实现最小的距离，松鼠应该先摘 [2, 5] 位置的坚果。

示例 2：

输入：height = 1, width = 3, tree = [0,1], squirrel = [0,0], nuts = [[0,2]]
输出：3

 

提示：

  • 1 <= height, width <= 100
  • tree.length == 2
  • squirrel.length == 2
  • 1 <= nuts.length <= 5000
  • nuts[i].length == 2
  • 0 <= treer, squirrelr, nutir <= height
  • 0 <= treec, squirrelc, nutic <= width

解法

方法一：路径分析

我们观察松鼠的移动路径，可以发现，松鼠会首先移动到某个坚果的位置，然后移动到树的位置。接下来，松鼠的移动路径之和等于“其余坚果到树的位置之和”再乘以 $2$。

因此，我们只需要选出一个坚果，作为松鼠的第一个目标，使得其到树的位置之和最小，即可得到最小路径。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。其中 $n$ 为坚果的数量。

Python3

class Solution:
    def minDistance(
        self,
        height: int,
        width: int,
        tree: List[int],
        squirrel: List[int],
        nuts: List[List[int]],
    ) -> int:
        x, y, a, b = *tree, *squirrel
        s = sum(abs(i - x) + abs(j - y) for i, j in nuts) * 2
        ans = inf
        for i, j in nuts:
            c = abs(i - x) + abs(j - y)
            d = abs(i - a) + abs(j - b) + c
            ans = min(ans, s + d - c * 2)
        return ans

Java

class Solution {
    public int minDistance(int height, int width, int[] tree, int[] squirrel, int[][] nuts) {
        int ans = Integer.MAX_VALUE;
        int s = 0;
        for (int[] a : nuts) {
            s += f(a, tree);
        }
        s *= 2;
        for (int[] a : nuts) {
            int c = f(a, tree);
            int d = f(a, squirrel) + c;
            ans = Math.min(ans, s + d - c * 2);
        }
        return ans;
    }

    private int f(int[] a, int[] b) {
        return Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);
    }
}

C++

class Solution {
public:
    int minDistance(int height, int width, vector<int>& tree, vector<int>& squirrel, vector<vector<int>>& nuts) {
        int ans = INT_MAX;
        int s = 0;
        for (auto& a : nuts) {
            s += f(a, tree);
        }
        s *= 2;
        for (auto& a : nuts) {
            int c = f(a, tree);
            int d = f(a, squirrel) + c;
            ans = min(ans, s + d - c * 2);
        }
        return ans;
    }

    int f(vector<int>& a, vector<int>& b) {
        return abs(a[0] - b[0]) + abs(a[1] - b[1]);
    }
};

Go

func minDistance(height int, width int, tree []int, squirrel []int, nuts [][]int) int {
	f := func(a, b []int) int {
		return abs(a[0]-b[0]) + abs(a[1]-b[1])
	}
	ans := math.MaxInt32
	s := 0
	for _, a := range nuts {
		s += f(a, tree)
	}
	s *= 2
	for _, a := range nuts {
		c := f(a, tree)
		d := f(a, squirrel) + c
		ans = min(ans, s+d-c*2)
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}