Skip to content

Latest commit

 

History

History
514 lines (435 loc) · 12.1 KB

README_EN.md

File metadata and controls

514 lines (435 loc) · 12.1 KB
Raw
comments difficulty edit_url tags
true
Medium
Depth-First Search
Breadth-First Search
Union Find
Graph

684. Redundant Connection

中文文档

Description

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

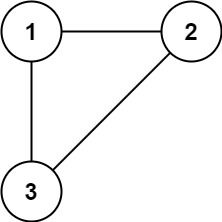
Example 1:

Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

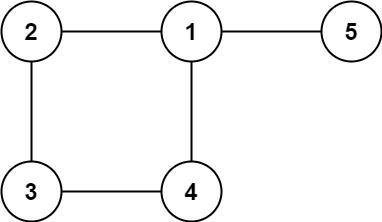
Example 2:

Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • There are no repeated edges.
  • The given graph is connected.

Solutions

Solution 1: Union-Find

According to the problem description, we need to find an edge that can be removed so that the remaining part is a tree with $n$ nodes. We can traverse each edge and determine whether the two nodes of this edge are in the same connected component. If they are in the same connected component, it means this edge is redundant and can be removed, so we directly return this edge. Otherwise, we merge the two nodes connected by this edge into the same connected component.

The time complexity is $O(n \log n)$, and the space complexity is $O(n)$. Here, $n$ is the number of edges.

Python3

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        def find(x: int) -> int:
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(len(edges)))
        for a, b in edges:
            pa, pb = find(a - 1), find(b - 1)
            if pa == pb:
                return [a, b]
            p[pa] = pb

Java

class Solution {
    private int[] p;

    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        for (int i = 0;; ++i) {
            int pa = find(edges[i][0] - 1);
            int pb = find(edges[i][1] - 1);
            if (pa == pb) {
                return edges[i];
            }
            p[pa] = pb;
        }
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        function<int(int)> find = [&](int x) {
            return x == p[x] ? x : p[x] = find(p[x]);
        };
        for (int i = 0;; ++i) {
            int pa = find(edges[i][0] - 1);
            int pb = find(edges[i][1] - 1);
            if (pa == pb) {
                return edges[i];
            }
            p[pa] = pb;
        }
    }
};

Go

func findRedundantConnection(edges [][]int) []int {
	n := len(edges)
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for i := 0; ; i++ {
		pa, pb := find(edges[i][0]-1), find(edges[i][1]-1)
		if pa == pb {
			return edges[i]
		}
		p[pa] = pb
	}
}

TypeScript

function findRedundantConnection(edges: number[][]): number[] {
    const n = edges.length;
    const p: number[] = Array.from({ length: n }, (_, i) => i);
    const find = (x: number): number => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    for (let i = 0; ; ++i) {
        const pa = find(edges[i][0] - 1);
        const pb = find(edges[i][1] - 1);
        if (pa === pb) {
            return edges[i];
        }
        p[pa] = pb;
    }
}

JavaScript

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function (edges) {
    const n = edges.length;
    const p = Array.from({ length: n }, (_, i) => i);
    const find = x => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    for (let i = 0; ; ++i) {
        const pa = find(edges[i][0] - 1);
        const pb = find(edges[i][1] - 1);
        if (pa === pb) {
            return edges[i];
        }
        p[pa] = pb;
    }
};

Solution 2: Union-Find (Template Approach)

Here is a template approach using Union-Find for your reference.

The time complexity is $O(n \alpha(n))$, and the space complexity is $O(n)$. Here, $n$ is the number of edges, and $\alpha(n)$ is the inverse Ackermann function, which can be considered a very small constant.

Python3

class UnionFind:
    __slots__ = "p", "size"

    def __init__(self, n: int):
        self.p: List[int] = list(range(n))
        self.size: List[int] = [1] * n

    def find(self, x: int) -> int:
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a: int, b: int) -> bool:
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.size[pa] > self.size[pb]:
            self.p[pb] = pa
            self.size[pa] += self.size[pb]
        else:
            self.p[pa] = pb
            self.size[pb] += self.size[pa]
        return True


class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        uf = UnionFind(len(edges))
        for a, b in edges:
            if not uf.union(a - 1, b - 1):
                return [a, b]

Java

class UnionFind {
    private final int[] p;
    private final int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public boolean union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }
}

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        UnionFind uf = new UnionFind(edges.length);
        for (int i = 0;; ++i) {
            if (!uf.union(edges[i][0] - 1, edges[i][1] - 1)) {
                return edges[i];
            }
        }
    }
}

C++

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        UnionFind uf(edges.size());
        for (int i = 0;; ++i) {
            if (!uf.unite(edges[i][0] - 1, edges[i][1] - 1)) {
                return edges[i];
            }
        }
    }
};

Go

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a), uf.find(b)
	if pa == pb {
		return false
	}
	if uf.size[pa] > uf.size[pb] {
		uf.p[pb] = pa
		uf.size[pa] += uf.size[pb]
	} else {
		uf.p[pa] = pb
		uf.size[pb] += uf.size[pa]
	}
	return true
}

func findRedundantConnection(edges [][]int) []int {
	uf := newUnionFind(len(edges))
	for i := 0; ; i++ {
		if !uf.union(edges[i][0]-1, edges[i][1]-1) {
			return edges[i]
		}
	}
}

TypeScript

class UnionFind {
    p: number[];
    size: number[];
    constructor(n: number) {
        this.p = Array.from({ length: n }, (_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const [pa, pb] = [this.find(a), this.find(b)];
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }
}

function findRedundantConnection(edges: number[][]): number[] {
    const uf = new UnionFind(edges.length);
    for (let i = 0; ; ++i) {
        if (!uf.union(edges[i][0] - 1, edges[i][1] - 1)) {
            return edges[i];
        }
    }
}

JavaScript

class UnionFind {
    constructor(n) {
        this.p = Array.from({ length: n }, (_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x) {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a, b) {
        const pa = this.find(a);
        const pb = this.find(b);
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }
}

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function (edges) {
    const uf = new UnionFind(edges.length);
    for (let i = 0; i < edges.length; i++) {
        if (!uf.union(edges[i][0] - 1, edges[i][1] - 1)) {
            return edges[i];
        }
    }
};