README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0700-0799/0750.Number%20Of%20Corner%20Rectangles/README.md	数组 数学 动态规划 矩阵

750. 角矩形的数量 🔒

English Version

题目描述

给定一个只包含 0 和 1 的 m x n 整数矩阵 grid ，返回 其中 「角矩形 」的数量 。

一个「角矩形」是由四个不同的在矩阵上的 1 形成的 轴对齐 的矩形。注意只有角的位置才需要为 1。

注意：4 个 1 的位置需要是不同的。

 

示例 1：

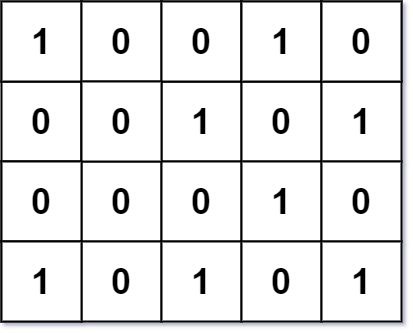
输入：grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]]
输出：1
解释：只有一个角矩形，角的位置为 grid[1][2], grid[1][4], grid[3][2], grid[3][4]。

示例 2：

输入：grid = [[1,1,1],[1,1,1],[1,1,1]]
输出：9
解释：这里有 4 个 2x2 的矩形，4 个 2x3 和 3x2 的矩形和 1 个 3x3 的矩形。

示例 3：

输入：grid = [[1,1,1,1]]
输出：0
解释：矩形必须有 4 个不同的角。

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• grid[i][j] 不是 0 就是 1
• 网格中 1 的个数在 [1, 6000] 范围内

解法

方法一：哈希表 + 枚举

我们枚举每一行作为矩形的下边，对于当前行，如果列 $i$ 和列 $j$ 都是 $1$，那么我们用哈希表找出此前的所有行中，有多少行的 $i$ 和 $j$ 列都是 $1$，那么就有多少个以 $(i, j)$ 为右下角的矩形，我们将其数量加入答案。然后将 $(i, j)$ 加入哈希表，继续枚举下一对 $(i, j)$。

时间复杂度 $O(m \times n^2)$，空间复杂度 $O(n^2)$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

Python3

class Solution:
    def countCornerRectangles(self, grid: List[List[int]]) -> int:
        ans = 0
        cnt = Counter()
        n = len(grid[0])
        for row in grid:
            for i, c1 in enumerate(row):
                if c1:
                    for j in range(i + 1, n):
                        if row[j]:
                            ans += cnt[(i, j)]
                            cnt[(i, j)] += 1
        return ans

Java

class Solution {
    public int countCornerRectangles(int[][] grid) {
        int n = grid[0].length;
        int ans = 0;
        Map<List<Integer>, Integer> cnt = new HashMap<>();
        for (var row : grid) {
            for (int i = 0; i < n; ++i) {
                if (row[i] == 1) {
                    for (int j = i + 1; j < n; ++j) {
                        if (row[j] == 1) {
                            List<Integer> t = List.of(i, j);
                            ans += cnt.getOrDefault(t, 0);
                            cnt.merge(t, 1, Integer::sum);
                        }
                    }
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int countCornerRectangles(vector<vector<int>>& grid) {
        int n = grid[0].size();
        int ans = 0;
        map<pair<int, int>, int> cnt;
        for (auto& row : grid) {
            for (int i = 0; i < n; ++i) {
                if (row[i]) {
                    for (int j = i + 1; j < n; ++j) {
                        if (row[j]) {
                            ans += cnt[{i, j}];
                            ++cnt[{i, j}];
                        }
                    }
                }
            }
        }
        return ans;
    }
};

Go

func countCornerRectangles(grid [][]int) (ans int) {
	n := len(grid[0])
	type pair struct{ x, y int }
	cnt := map[pair]int{}
	for _, row := range grid {
		for i, x := range row {
			if x == 1 {
				for j := i + 1; j < n; j++ {
					if row[j] == 1 {
						t := pair{i, j}
						ans += cnt[t]
						cnt[t]++
					}
				}
			}
		}
	}
	return
}

TypeScript

function countCornerRectangles(grid: number[][]): number {
    const n = grid[0].length;
    let ans = 0;
    const cnt: Map<number, number> = new Map();
    for (const row of grid) {
        for (let i = 0; i < n; ++i) {
            if (row[i] === 1) {
                for (let j = i + 1; j < n; ++j) {
                    if (row[j] === 1) {
                        const t = i * 200 + j;
                        ans += cnt.get(t) ?? 0;
                        cnt.set(t, (cnt.get(t) ?? 0) + 1);
                    }
                }
            }
        }
    }
    return ans;
}