README.md

comments	difficulty	edit_url	tags
true	简单	https://github.com/doocs/leetcode/edit/main/solution/0900-0999/0941.Valid%20Mountain%20Array/README.md	数组

941. 有效的山脉数组

English Version

题目描述

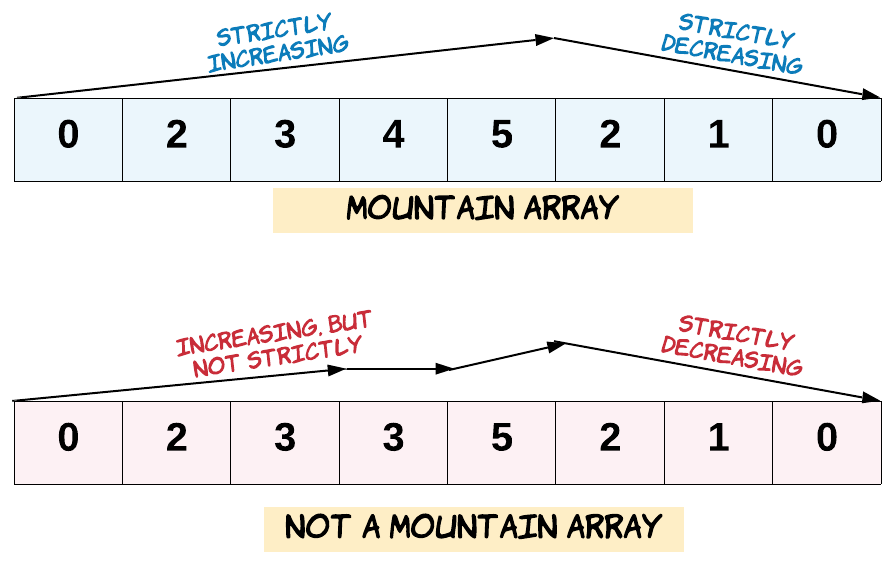
给定一个整数数组 arr，如果它是有效的山脉数组就返回 true，否则返回 false。

让我们回顾一下，如果 arr 满足下述条件，那么它是一个山脉数组：

• arr.length >= 3
• 在 0 < i < arr.length - 1 条件下，存在 i 使得：
  • arr[0] < arr[1] < ... arr[i-1] < arr[i]
  • arr[i] > arr[i+1] > ... > arr[arr.length - 1]

 

 

示例 1：

输入：arr = [2,1]
输出：false

示例 2：

输入：arr = [3,5,5]
输出：false

示例 3：

输入：arr = [0,3,2,1]
输出：true

 

提示：

• 1 <= arr.length <= 104
• 0 <= arr[i] <= 104

解法

方法一：双指针

我们首先判断数组的长度是否小于 $3$，如果小于 $3$，那么一定不是山脉数组，直接返回 false。

然后，我们使用指针 $i$ 从数组的左端开始向右移动，直到找到一个位置 $i$，使得 $arr[i] > arr[i + 1]$。然后，我们使用指针 $j$ 从数组的右端开始向左移动，直到找到一个位置 $j$，使得 $arr[j] > arr[j - 1]$。如果满足条件 $i = j$，那么就说明数组 $arr$ 是一个山脉数组。

时间复杂度 $O(n)$，其中 $n$ 是数组的长度。空间复杂度 $O(1)$。

Python3

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        n = len(arr)
        if n < 3:
            return False
        i, j = 0, n - 1
        while i + 1 < n - 1 and arr[i] < arr[i + 1]:
            i += 1
        while j - 1 > 0 and arr[j - 1] > arr[j]:
            j -= 1
        return i == j

Java

class Solution {
    public boolean validMountainArray(int[] arr) {
        int n = arr.length;
        if (n < 3) {
            return false;
        }
        int i = 0, j = n - 1;
        while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
            ++i;
        }
        while (j - 1 > 0 && arr[j - 1] > arr[j]) {
            --j;
        }
        return i == j;
    }
}

C++

class Solution {
public:
    bool validMountainArray(vector<int>& arr) {
        int n = arr.size();
        if (n < 3) {
            return false;
        }
        int i = 0, j = n - 1;
        while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
            ++i;
        }
        while (j - 1 > 0 && arr[j - 1] > arr[j]) {
            --j;
        }
        return i == j;
    }
};

Go

func validMountainArray(arr []int) bool {
	n := len(arr)
	if n < 3 {
		return false
	}
	i, j := 0, n-1
	for i+1 < n-1 && arr[i] < arr[i+1] {
		i++
	}
	for j-1 > 0 && arr[j-1] > arr[j] {
		j--
	}
	return i == j
}

TypeScript

function validMountainArray(arr: number[]): boolean {
    const n = arr.length;
    if (n < 3) {
        return false;
    }
    let [i, j] = [0, n - 1];
    while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
        i++;
    }
    while (j - 1 > 0 && arr[j] < arr[j - 1]) {
        j--;
    }
    return i === j;
}