README.md

comments	difficulty	edit_url	rating	source	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/1000-1099/1035.Uncrossed%20Lines/README.md	1805	第 134 场周赛 Q3	数组 动态规划

1035. 不相交的线

English Version

题目描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

•  nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

 

示例 1：

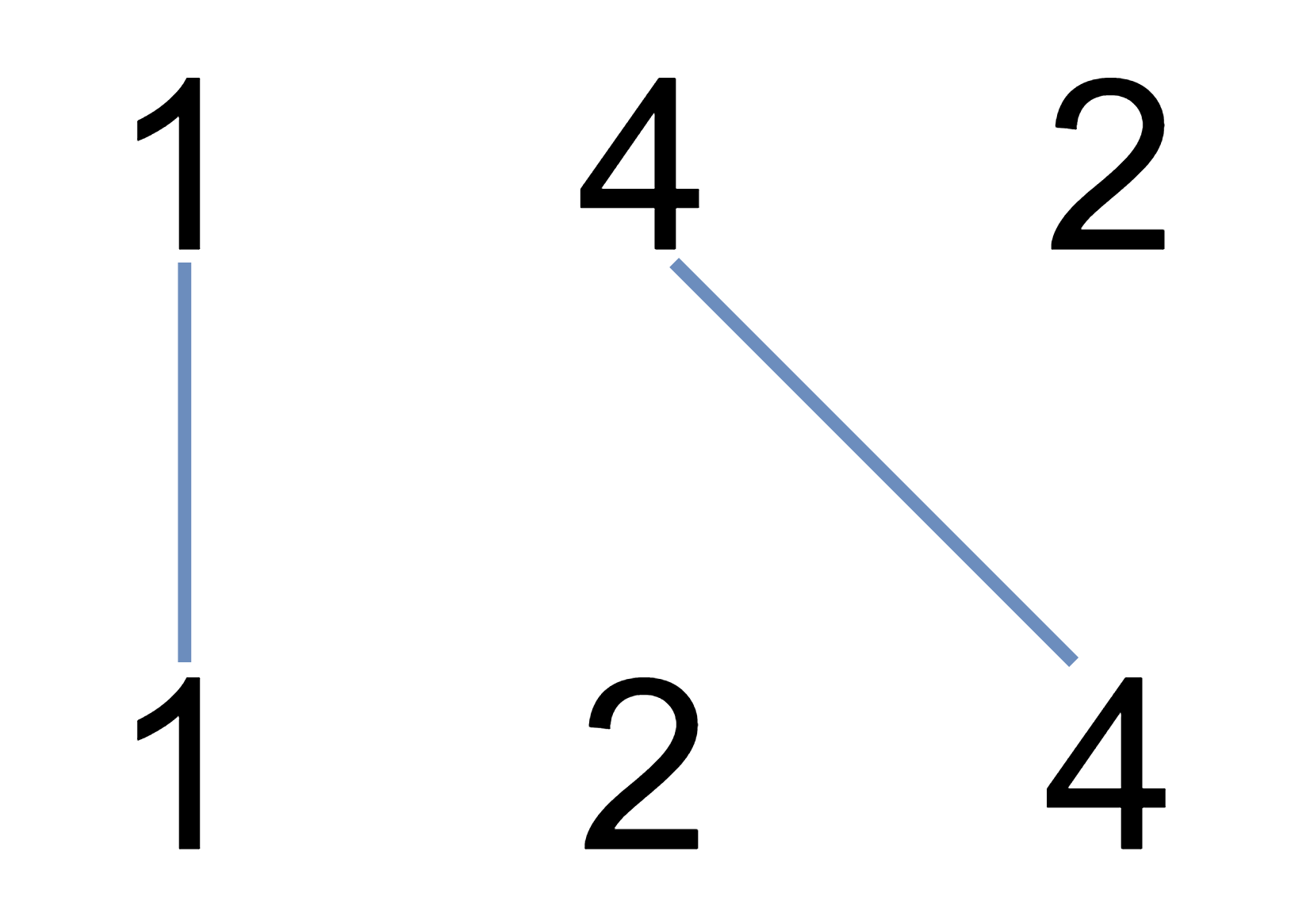
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

 

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

 

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示 $\textit{nums1}$ 前 $i$ 个数和 $\textit{nums2}$ 前 $j$ 个数的最大连线数。初始时 $f[i][j] = 0$，答案即为 $f[m][n]$。

当 $\textit{nums1}[i-1] = \textit{nums2}[j-1]$ 时，我们可以在 $\textit{nums1}$ 的前 $i-1$ 个数和 $\textit{nums2}$ 的前 $j-1$ 个数的基础上增加一条连线，此时 $f[i][j] = f[i-1][j-1] + 1$。

当 $\textit{nums1}[i-1] \neq \textit{nums2}[j-1]$ 时，我们要么在 $\textit{nums1}$ 的前 $i-1$ 个数和 $\textit{nums2}$ 的前 $j$ 个数的基础上求解，要么在 $\textit{nums1}$ 的前 $i$ 个数和 $\textit{nums2}$ 的前 $j-1$ 个数的基础上求解，取两者的最大值，即 $f[i][j] = \max(f[i-1][j], f[i][j-1])$。

最后返回 $f[m][n]$ 即可。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是 $\textit{nums1}$ 和 $\textit{nums2}$ 的长度。

Python3

class Solution:
    def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
        m, n = len(nums1), len(nums2)
        f = [[0] * (n + 1) for _ in range(m + 1)]
        for i, x in enumerate(nums1, 1):
            for j, y in enumerate(nums2, 1):
                if x == y:
                    f[i][j] = f[i - 1][j - 1] + 1
                else:
                    f[i][j] = max(f[i - 1][j], f[i][j - 1])
        return f[m][n]

Java

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int[][] f = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    f[i][j] = f[i - 1][j - 1] + 1;
                } else {
                    f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
                }
            }
        }
        return f[m][n];
    }
}

C++

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        int f[m + 1][n + 1];
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    f[i][j] = f[i - 1][j - 1] + 1;
                } else {
                    f[i][j] = max(f[i - 1][j], f[i][j - 1]);
                }
            }
        }
        return f[m][n];
    }
};

Go

func maxUncrossedLines(nums1 []int, nums2 []int) int {
	m, n := len(nums1), len(nums2)
	f := make([][]int, m+1)
	for i := range f {
		f[i] = make([]int, n+1)
	}
	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			if nums1[i-1] == nums2[j-1] {
				f[i][j] = f[i-1][j-1] + 1
			} else {
				f[i][j] = max(f[i-1][j], f[i][j-1])
			}
		}
	}
	return f[m][n]
}

TypeScript

function maxUncrossedLines(nums1: number[], nums2: number[]): number {
    const m = nums1.length;
    const n = nums2.length;
    const f: number[][] = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0));
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            if (nums1[i - 1] === nums2[j - 1]) {
                f[i][j] = f[i - 1][j - 1] + 1;
            } else {
                f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
            }
        }
    }
    return f[m][n];
}

JavaScript

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var maxUncrossedLines = function (nums1, nums2) {
    const m = nums1.length;
    const n = nums2.length;
    const f = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0));
    for (let i = 1; i <= m; ++i) {
        for (let j = 1; j <= n; ++j) {
            if (nums1[i - 1] === nums2[j - 1]) {
                f[i][j] = f[i - 1][j - 1] + 1;
            } else {
                f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
            }
        }
    }
    return f[m][n];
};