| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1666 |
第 150 场周赛 Q3 |
|
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
示例 1:
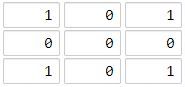
输入:grid = [[1,0,1],[0,0,0],[1,0,1]] 输出:2 解释: 海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
示例 2:
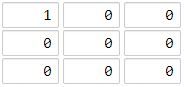
输入:grid = [[1,0,0],[0,0,0],[0,0,0]] 输出:4 解释: 海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大,最大距离为 4。
提示:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]不是0就是1
我们可以将所有陆地单元格加入队列
否则,我们从陆地单元格开始进行广度优先搜索。定义初始步数
在每一轮搜索中,我们将队列中的所有单元格向四个方向扩散,若单元格是海洋单元格,则将其标记为陆地单元格,并加入队列。在一轮扩散完成后,我们将步数加
最后,我们返回步数
时间复杂度
class Solution:
def maxDistance(self, grid: List[List[int]]) -> int:
n = len(grid)
q = deque((i, j) for i in range(n) for j in range(n) if grid[i][j])
ans = -1
if len(q) in (0, n * n):
return ans
dirs = (-1, 0, 1, 0, -1)
while q:
for _ in range(len(q)):
i, j = q.popleft()
for a, b in pairwise(dirs):
x, y = i + a, j + b
if 0 <= x < n and 0 <= y < n and grid[x][y] == 0:
grid[x][y] = 1
q.append((x, y))
ans += 1
return ansclass Solution {
public int maxDistance(int[][] grid) {
int n = grid.length;
Deque<int[]> q = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
q.offer(new int[] {i, j});
}
}
}
int ans = -1;
if (q.isEmpty() || q.size() == n * n) {
return ans;
}
int[] dirs = {-1, 0, 1, 0, -1};
while (!q.isEmpty()) {
for (int i = q.size(); i > 0; --i) {
int[] p = q.poll();
for (int k = 0; k < 4; ++k) {
int x = p[0] + dirs[k], y = p[1] + dirs[k + 1];
if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0) {
grid[x][y] = 1;
q.offer(new int[] {x, y});
}
}
}
++ans;
}
return ans;
}
}class Solution {
public:
int maxDistance(vector<vector<int>>& grid) {
int n = grid.size();
queue<pair<int, int>> q;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j]) {
q.emplace(i, j);
}
}
}
int ans = -1;
if (q.empty() || q.size() == n * n) {
return ans;
}
int dirs[5] = {-1, 0, 1, 0, -1};
while (!q.empty()) {
for (int m = q.size(); m; --m) {
auto [i, j] = q.front();
q.pop();
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < n && y >= 0 && y < n && !grid[x][y]) {
grid[x][y] = 1;
q.emplace(x, y);
}
}
}
++ans;
}
return ans;
}
};func maxDistance(grid [][]int) int {
n := len(grid)
q := [][2]int{}
for i, row := range grid {
for j, v := range row {
if v == 1 {
q = append(q, [2]int{i, j})
}
}
}
ans := -1
if len(q) == 0 || len(q) == n*n {
return ans
}
dirs := [5]int{-1, 0, 1, 0, -1}
for len(q) > 0 {
for i := len(q); i > 0; i-- {
p := q[0]
q = q[1:]
for k := 0; k < 4; k++ {
x, y := p[0]+dirs[k], p[1]+dirs[k+1]
if x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0 {
grid[x][y] = 1
q = append(q, [2]int{x, y})
}
}
}
ans++
}
return ans
}function maxDistance(grid: number[][]): number {
const n = grid.length;
const q: [number, number][] = [];
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 1) {
q.push([i, j]);
}
}
}
let ans = -1;
if (q.length === 0 || q.length === n * n) {
return ans;
}
const dirs: number[] = [-1, 0, 1, 0, -1];
while (q.length > 0) {
for (let m = q.length; m; --m) {
const [i, j] = q.shift()!;
for (let k = 0; k < 4; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] === 0) {
grid[x][y] = 1;
q.push([x, y]);
}
}
}
++ans;
}
return ans;
}