comments

difficulty

edit_url

rating

source

1263. 推箱子

English Version

题目描述

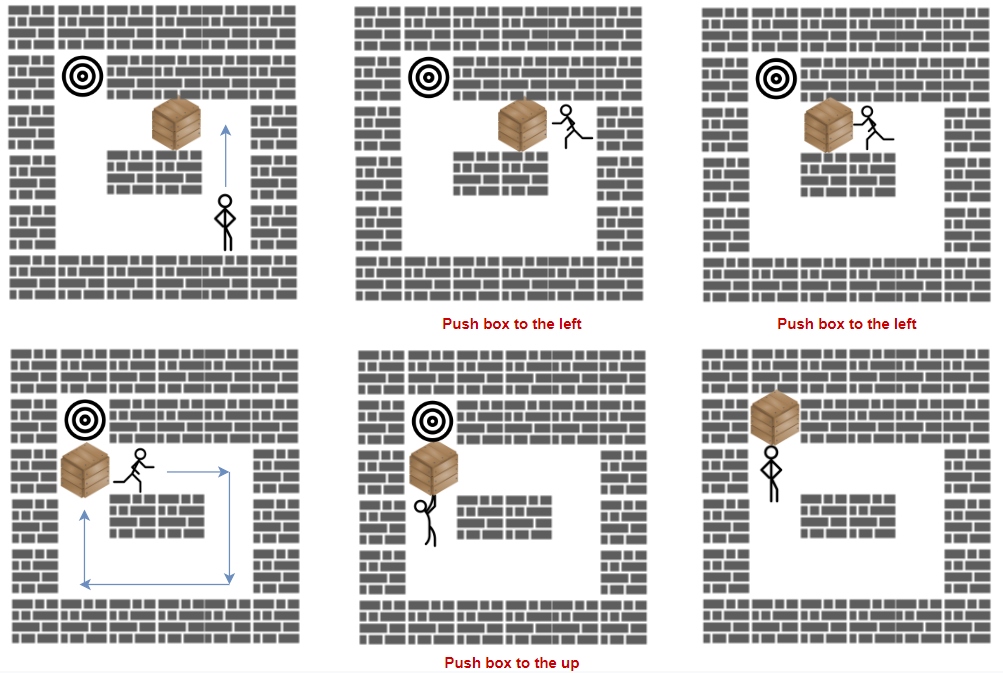
「推箱子」是一款风靡全球的益智小游戏，玩家需要将箱子推到仓库中的目标位置。

游戏地图用大小为 m x n 的网格 grid 表示，其中每个元素可以是墙、地板或者是箱子。

现在你将作为玩家参与游戏，按规则将箱子 'B' 移动到目标位置 'T' ：

玩家用字符 'S' 表示，只要他在地板上，就可以在网格中向上、下、左、右四个方向移动。
地板用字符 '.' 表示，意味着可以自由行走。
墙用字符 '#' 表示，意味着障碍物，不能通行。
箱子仅有一个，用字符 'B' 表示。相应地，网格上有一个目标位置 'T'。
玩家需要站在箱子旁边，然后沿着箱子的方向进行移动，此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。

返回将箱子推到目标位置的最小推动次数，如果无法做到，请返回 -1。

示例 1：

输入：grid = [["#","#","#","#","#","#"],
             ["#","T","#","#","#","#"],
             ["#",".",".","B",".","#"],
             ["#",".","#","#",".","#"],
             ["#",".",".",".","S","#"],
             ["#","#","#","#","#","#"]]
输出：3
解释：我们只需要返回推箱子的次数。

示例 2：

输入：grid = [["#","#","#","#","#","#"],
             ["#","T","#","#","#","#"],
             ["#",".",".","B",".","#"],
             ["#","#","#","#",".","#"],
             ["#",".",".",".","S","#"],
             ["#","#","#","#","#","#"]]
输出：-1

示例 3：

输入：grid = [["#","#","#","#","#","#"],
             ["#","T",".",".","#","#"],
             ["#",".","#","B",".","#"],
             ["#",".",".",".",".","#"],
             ["#",".",".",".","S","#"],
             ["#","#","#","#","#","#"]]
输出：5
解释：向下、向左、向左、向上再向上。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 20
grid 仅包含字符 '.', '#', 'S' , 'T', 以及 'B'。
grid 中 'S', 'B' 和 'T' 各只能出现一个。

解法

方法一：双端队列 + BFS

我们把玩家的位置和箱子的位置看成一个状态，即 $(s_i, s_j, b_i, b_j)$，其中 $(s_i, s_j)$ 是玩家的位置，而 $(b_i, b_j)$ 是箱子的位置。在代码实现上，我们定义一个函数 $f(i, j)$，它将二维坐标 $(i, j)$ 映射到一个一维的状态编号，即 $f(i, j) = i \times n + j$，其中 $n$ 是网格的列数。那么玩家和箱子的状态就是 $(f(s_i, s_j), f(b_i, b_j))$。

我们首先遍历网格，找到玩家和箱子的初始位置，记为 $(s_i, s_j)$ 和 $(b_i, b_j)$。

然后，我们定义一个双端队列 $q$，其中每个元素都是一个三元组 $(f(s_i, s_j), f(b_i, b_j), d)$，表示玩家位于 $(s_i, s_j)$，箱子位于 $(b_i, b_j)$，并且已经进行了 $d$ 次推动。初始时，我们将 $(f(s_i, s_j), f(b_i, b_j), 0)$ 加入队列 $q$。

另外，我们用一个二维数组 $vis$ 记录每个状态是否已经访问过，初始时 $vis[f(s_i, s_j), f(b_i, b_j)]$ 标记为已访问。

接下来，我们开始进行广度优先搜索。

在每一步搜索中，我们取出队头元素 $(f(s_i, s_j), f(b_i, b_j), d)$，并检查是否满足 $grid[b_i][b_j] = 'T'$，如果是，说明箱子已经被推到目标位置，此时将 $d$ 作为答案返回即可。

否则，我们枚举玩家的下一步移动方向，玩家新的位置记为 $(s_x, s_y)$，如果 $(s_x, s_y)$ 是一个合法的位置，我们判断此时 $(s_x, s_y)$ 是否与箱子的位置 $(b_i, b_j)$ 相同：

如果相同，说明当前玩家到达了箱子的位置，并且推动箱子往前走了一步。箱子新的位置为 $(b_x, b_y)$，如果 $(b_x, b_y)$ 是一个合法的位置，且状态 $(f(s_x, s_y), f(b_x, b_y))$ 没有被访问过，那么我们就将 $(f(s_x, s_y), f(b_x, b_y), d + 1)$ 加入队列 $q$ 的末尾，并将 $vis[f(s_x, s_y), f(b_x, b_y)]$ 标记为已访问。
如果不同，说明当前玩家没有推动箱子，那么我们只需要判断状态 $(f(s_x, s_y), f(b_i, b_j))$ 是否被访问过，如果没有被访问过，那么我们就将 $(f(s_x, s_y), f(b_i, b_j), d)$ 加入队列 $q$ 的头部，并将 $vis[f(s_x, s_y), f(b_i, b_j)]$ 标记为已访问。

继续进行广度优先搜索，直到队列为空为止。

注意，如果推动箱子，那么推动次数 $d$ 需要加 $1$，并且新的状态加入到队列 $q$ 的末尾；如果没推动箱子，那么推动次数 $d$ 不变，新的状态加入到队列 $q$ 的头部。

最后，如果没有找到合法的推动方案，那么返回 $-1$。

时间复杂度 $O(m^2 \times n^2)$，空间复杂度 $O(m^2 \times n^2)$。其中 $m$ 和 $n$ 分别是网格的行数和列数。

Python3

class Solution:
    def minPushBox(self, grid: List[List[str]]) -> int:
        def f(i: int, j: int) -> int:
            return i * n + j

        def check(i: int, j: int) -> bool:
            return 0 <= i < m and 0 <= j < n and grid[i][j] != "#"

        for i, row in enumerate(grid):
            for j, c in enumerate(row):
                if c == "S":
                    si, sj = i, j
                elif c == "B":
                    bi, bj = i, j
        m, n = len(grid), len(grid[0])
        dirs = (-1, 0, 1, 0, -1)
        q = deque([(f(si, sj), f(bi, bj), 0)])
        vis = [[False] * (m * n) for _ in range(m * n)]
        vis[f(si, sj)][f(bi, bj)] = True
        while q:
            s, b, d = q.popleft()
            bi, bj = b // n, b % n
            if grid[bi][bj] == "T":
                return d
            si, sj = s // n, s % n
            for a, b in pairwise(dirs):
                sx, sy = si + a, sj + b
                if not check(sx, sy):
                    continue
                if sx == bi and sy == bj:
                    bx, by = bi + a, bj + b
                    if not check(bx, by) or vis[f(sx, sy)][f(bx, by)]:
                        continue
                    vis[f(sx, sy)][f(bx, by)] = True
                    q.append((f(sx, sy), f(bx, by), d + 1))
                elif not vis[f(sx, sy)][f(bi, bj)]:
                    vis[f(sx, sy)][f(bi, bj)] = True
                    q.appendleft((f(sx, sy), f(bi, bj), d))
        return -1

Java

class Solution {
    private int m;
    private int n;
    private char[][] grid;

    public int minPushBox(char[][] grid) {
        m = grid.length;
        n = grid[0].length;
        this.grid = grid;
        int si = 0, sj = 0, bi = 0, bj = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 'S') {
                    si = i;
                    sj = j;
                } else if (grid[i][j] == 'B') {
                    bi = i;
                    bj = j;
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        Deque<int[]> q = new ArrayDeque<>();
        boolean[][] vis = new boolean[m * n][m * n];
        q.offer(new int[] {f(si, sj), f(bi, bj), 0});
        vis[f(si, sj)][f(bi, bj)] = true;
        while (!q.isEmpty()) {
            var p = q.poll();
            int d = p[2];
            bi = p[1] / n;
            bj = p[1] % n;
            if (grid[bi][bj] == 'T') {
                return d;
            }
            si = p[0] / n;
            sj = p[0] % n;
            for (int k = 0; k < 4; ++k) {
                int sx = si + dirs[k], sy = sj + dirs[k + 1];
                if (!check(sx, sy)) {
                    continue;
                }
                if (sx == bi && sy == bj) {
                    int bx = bi + dirs[k], by = bj + dirs[k + 1];
                    if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
                        continue;
                    }
                    vis[f(sx, sy)][f(bx, by)] = true;
                    q.offer(new int[] {f(sx, sy), f(bx, by), d + 1});
                } else if (!vis[f(sx, sy)][f(bi, bj)]) {
                    vis[f(sx, sy)][f(bi, bj)] = true;
                    q.offerFirst(new int[] {f(sx, sy), f(bi, bj), d});
                }
            }
        }
        return -1;
    }

    private int f(int i, int j) {
        return i * n + j;
    }

    private boolean check(int i, int j) {
        return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#';
    }
}

C++

class Solution {
public:
    int minPushBox(vector<vector<char>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int si, sj, bi, bj;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 'S') {
                    si = i, sj = j;
                } else if (grid[i][j] == 'B') {
                    bi = i, bj = j;
                }
            }
        }
        auto f = [&](int i, int j) {
            return i * n + j;
        };
        auto check = [&](int i, int j) {
            return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#';
        };
        int dirs[5] = {-1, 0, 1, 0, -1};
        deque<tuple<int, int, int>> q;
        q.emplace_back(f(si, sj), f(bi, bj), 0);
        bool vis[m * n][m * n];
        memset(vis, false, sizeof(vis));
        vis[f(si, sj)][f(bi, bj)] = true;
        while (!q.empty()) {
            auto [s, b, d] = q.front();
            q.pop_front();
            si = s / n, sj = s % n;
            bi = b / n, bj = b % n;
            if (grid[bi][bj] == 'T') {
                return d;
            }
            for (int k = 0; k < 4; ++k) {
                int sx = si + dirs[k], sy = sj + dirs[k + 1];
                if (!check(sx, sy)) {
                    continue;
                }
                if (sx == bi && sy == bj) {
                    int bx = bi + dirs[k], by = bj + dirs[k + 1];
                    if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
                        continue;
                    }
                    vis[f(sx, sy)][f(bx, by)] = true;
                    q.emplace_back(f(sx, sy), f(bx, by), d + 1);
                } else if (!vis[f(sx, sy)][f(bi, bj)]) {
                    vis[f(sx, sy)][f(bi, bj)] = true;
                    q.emplace_front(f(sx, sy), f(bi, bj), d);
                }
            }
        }
        return -1;
    }
};

Go

func minPushBox(grid [][]byte) int {
	m, n := len(grid), len(grid[0])
	var si, sj, bi, bj int
	for i, row := range grid {
		for j, c := range row {
			if c == 'S' {
				si, sj = i, j
			} else if c == 'B' {
				bi, bj = i, j
			}
		}
	}
	f := func(i, j int) int {
		return i*n + j
	}
	check := func(i, j int) bool {
		return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#'
	}
	q := [][]int{[]int{f(si, sj), f(bi, bj), 0}}
	vis := make([][]bool, m*n)
	for i := range vis {
		vis[i] = make([]bool, m*n)
	}
	vis[f(si, sj)][f(bi, bj)] = true
	dirs := [5]int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		si, sj, bi, bj = p[0]/n, p[0]%n, p[1]/n, p[1]%n
		d := p[2]
		if grid[bi][bj] == 'T' {
			return d
		}
		for k := 0; k < 4; k++ {
			sx, sy := si+dirs[k], sj+dirs[k+1]
			if !check(sx, sy) {
				continue
			}
			if sx == bi && sy == bj {
				bx, by := bi+dirs[k], bj+dirs[k+1]
				if !check(bx, by) || vis[f(sx, sy)][f(bx, by)] {
					continue
				}
				vis[f(sx, sy)][f(bx, by)] = true
				q = append(q, []int{f(sx, sy), f(bx, by), d + 1})
			} else if !vis[f(sx, sy)][f(bi, bj)] {
				vis[f(sx, sy)][f(bi, bj)] = true
				q = append([][]int{[]int{f(sx, sy), f(bi, bj), d}}, q...)
			}
		}
	}
	return -1
}

TypeScript

function minPushBox(grid: string[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    let [si, sj, bi, bj] = [0, 0, 0, 0];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 'S') {
                [si, sj] = [i, j];
            } else if (grid[i][j] === 'B') {
                [bi, bj] = [i, j];
            }
        }
    }
    const f = (i: number, j: number): number => i * n + j;
    const check = (i: number, j: number): boolean =>
        i >= 0 && i < m && j >= 0 && j < n && grid[i][j] !== '#';

    const q: Deque<[number, number, number]> = new Deque();
    const vis: boolean[][] = new Array(m * n).fill(0).map(() => new Array(m * n).fill(false));
    q.push([f(si, sj), f(bi, bj), 0]);
    vis[f(si, sj)][f(bi, bj)] = true;
    const dirs: number[] = [-1, 0, 1, 0, -1];
    while (q.size() > 0) {
        const [s, b, d] = q.shift()!;
        const [si, sj] = [Math.floor(s / n), s % n];
        const [bi, bj] = [Math.floor(b / n), b % n];
        if (grid[bi][bj] === 'T') {
            return d;
        }
        for (let k = 0; k < 4; ++k) {
            const [sx, sy] = [si + dirs[k], sj + dirs[k + 1]];
            if (!check(sx, sy)) {
                continue;
            }
            if (sx === bi && sy === bj) {
                const [bx, by] = [bi + dirs[k], bj + dirs[k + 1]];
                if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
                    continue;
                }
                vis[f(sx, sy)][f(bx, by)] = true;
                q.push([f(sx, sy), f(bx, by), d + 1]);
            } else if (!vis[f(sx, sy)][f(bi, bj)]) {
                vis[f(sx, sy)][f(bi, bj)] = true;
                q.unshift([f(sx, sy), f(bi, bj), d]);
            }
        }
    }
    return -1;
}

/* 以下是双向列队模板类 */
class CircularDeque<T> {
    prev: CircularDeque<T> | null;
    next: CircularDeque<T> | null;
    begin: number;
    end: number;
    empty: boolean;
    data: T[];
    constructor(N: number) {
        this.prev = this.next = null;
        this.begin = this.end = 0;
        this.empty = true;
        this.data = Array(N);
    }

    isFull(): boolean {
        return this.end === this.begin && !this.empty;
    }

    isEmpty(): boolean {
        return this.empty;
    }

    push(val: T): boolean {
        if (this.isFull()) return false;
        this.empty = false;
        this.data[this.end] = val;
        this.end = (this.end + 1) % this.data.length;
        return true;
    }

    front(): T | undefined {
        return this.isEmpty() ? undefined : this.data[this.begin];
    }

    back(): T | undefined {
        return this.isEmpty() ? undefined : this.data[this.end - 1];
    }

    pop(): T | undefined {
        if (this.isEmpty()) return undefined;
        const value = this.data[this.end - 1];
        this.end = (this.end - 1) % this.data.length;
        if (this.end < 0) this.end += this.data.length;
        if (this.end === this.begin) this.empty = true;
        return value;
    }

    unshift(val: T): boolean {
        if (this.isFull()) return false;
        this.empty = false;
        this.begin = (this.begin - 1) % this.data.length;
        if (this.begin < 0) this.begin += this.data.length;
        this.data[this.begin] = val;
        return true;
    }

    shift(): T | undefined {
        if (this.isEmpty()) return undefined;
        const value = this.data[this.begin];
        this.begin = (this.begin + 1) % this.data.length;
        if (this.end === this.begin) this.empty = true;
        return value;
    }

    *values(): Generator<T, void, undefined> {
        if (this.isEmpty()) return undefined;
        let i = this.begin;
        do {
            yield this.data[i];
            i = (i + 1) % this.data.length;
        } while (i !== this.end);
    }
}

class Deque<T> {
    head: CircularDeque<T>;
    tail: CircularDeque<T>;
    _size: number;
    constructor(collection: T[] = []) {
        this.head = new CircularDeque<T>(128);
        this.tail = new CircularDeque<T>(128);
        this.tail.empty = this.head.empty = false;
        this.tail.prev = this.head;
        this.head.next = this.tail;
        this._size = 0;
        for (const item of collection) this.push(item);
    }

    size(): number {
        return this._size;
    }

    push(val: T): void {
        let last = this.tail.prev!;
        if (last.isFull()) {
            const inserted = new CircularDeque<T>(128);

            this.tail.prev = inserted;
            inserted.next = this.tail;

            last.next = inserted;
            inserted.prev = last;

            last = inserted;
        }
        last.push(val);
        this._size++;
    }

    back(): T | undefined {
        if (this._size === 0) return;
        return this.tail.prev!.back();
    }

    pop(): T | undefined {
        if (this.head.next === this.tail) return undefined;
        const last = this.tail.prev!;
        const value = last.pop();
        if (last.isEmpty()) {
            this.tail.prev = last.prev;
            last.prev!.next = this.tail;
        }
        this._size--;
        return value;
    }

    unshift(val: T): void {
        let first = this.head.next!;
        if (first.isFull()) {
            const inserted = new CircularDeque<T>(128);

            this.head.next = inserted;
            inserted.prev = this.head;

            inserted.next = first;
            first.prev = inserted;

            first = inserted;
        }
        first.unshift(val);
        this._size++;
    }

    shift(): T | undefined {
        if (this.head.next === this.tail) return undefined;
        const first = this.head.next!;
        const value = first.shift();
        if (first.isEmpty()) {
            this.head.next = first.next;
            first.next!.prev = this.head;
        }
        this._size--;
        return value;
    }

    front(): T | undefined {
        if (this._size === 0) return undefined;
        return this.head.next!.front();
    }

    *values(): Generator<T, void, undefined> {
        let node = this.head.next!;
        while (node !== this.tail) {
            for (const value of node.values()) yield value;
            node = node.next!;
        }
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

1263. 推箱子

题目描述

解法

方法一：双端队列 + BFS

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

1263. 推箱子

题目描述

解法

方法一：双端队列 + BFS

Python3

Java

C++

Go

TypeScript