Skip to content

Latest commit

 

History

History
242 lines (203 loc) · 6.13 KB

README.md

File metadata and controls

242 lines (203 loc) · 6.13 KB
Raw
comments difficulty edit_url rating source tags
true
困难
1961
第 200 场周赛 Q4
贪心
数组
双指针
动态规划

1537. 最大得分

English Version

题目描述

你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。

一条 合法路径 定义如下：

  • 选择数组 nums1 或者 nums2 开始遍历（从下标 0 处开始）。
  • 从左到右遍历当前数组。
  • 如果你遇到了 nums1 和 nums2 中都存在的值，那么你可以切换路径到另一个数组对应数字处继续遍历（但在合法路径中重复数字只会被统计一次）。

得分 定义为合法路径中不同数字的和。

请你返回 所有可能 合法路径 中的最大得分。由于答案可能很大，请你将它对 10^9 + 7 取余后返回。

 

示例 1：

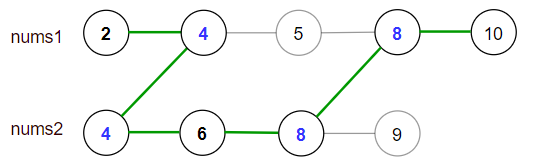
输入：nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
输出：30
解释：合法路径包括：
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],（从 nums1 开始遍历）
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10]  （从 nums2 开始遍历）
最大得分为上图中的绿色路径 [2,4,6,8,10] 。

示例 2：

输入：nums1 = [1,3,5,7,9], nums2 = [3,5,100]
输出：109
解释：最大得分由路径 [1,3,5,100] 得到。

示例 3：

输入：nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
输出：40
解释：nums1 和 nums2 之间无相同数字。
最大得分由路径[6,7,8,9,10]得到。

 

提示：

  • 1 <= nums1.length, nums2.length <= 105
  • 1 <= nums1[i], nums2[i] <= 107
  • nums1 和 nums2 都是严格递增的数组。

解法

方法一

Python3

class Solution:
    def maxSum(self, nums1: List[int], nums2: List[int]) -> int:
        mod = 10**9 + 7
        m, n = len(nums1), len(nums2)
        i = j = 0
        f = g = 0
        while i < m or j < n:
            if i == m:
                g += nums2[j]
                j += 1
            elif j == n:
                f += nums1[i]
                i += 1
            elif nums1[i] < nums2[j]:
                f += nums1[i]
                i += 1
            elif nums1[i] > nums2[j]:
                g += nums2[j]
                j += 1
            else:
                f = g = max(f, g) + nums1[i]
                i += 1
                j += 1
        return max(f, g) % mod

Java

class Solution {
    public int maxSum(int[] nums1, int[] nums2) {
        final int mod = (int) 1e9 + 7;
        int m = nums1.length, n = nums2.length;
        int i = 0, j = 0;
        long f = 0, g = 0;
        while (i < m || j < n) {
            if (i == m) {
                g += nums2[j++];
            } else if (j == n) {
                f += nums1[i++];
            } else if (nums1[i] < nums2[j]) {
                f += nums1[i++];
            } else if (nums1[i] > nums2[j]) {
                g += nums2[j++];
            } else {
                f = g = Math.max(f, g) + nums1[i];
                i++;
                j++;
            }
        }
        return (int) (Math.max(f, g) % mod);
    }
}

C++

class Solution {
public:
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        const int mod = 1e9 + 7;
        int m = nums1.size(), n = nums2.size();
        int i = 0, j = 0;
        long long f = 0, g = 0;
        while (i < m || j < n) {
            if (i == m) {
                g += nums2[j++];
            } else if (j == n) {
                f += nums1[i++];
            } else if (nums1[i] < nums2[j]) {
                f += nums1[i++];
            } else if (nums1[i] > nums2[j]) {
                g += nums2[j++];
            } else {
                f = g = max(f, g) + nums1[i];
                i++;
                j++;
            }
        }
        return max(f, g) % mod;
    }
};

Go

func maxSum(nums1 []int, nums2 []int) int {
	const mod int = 1e9 + 7
	m, n := len(nums1), len(nums2)
	i, j := 0, 0
	f, g := 0, 0
	for i < m || j < n {
		if i == m {
			g += nums2[j]
			j++
		} else if j == n {
			f += nums1[i]
			i++
		} else if nums1[i] < nums2[j] {
			f += nums1[i]
			i++
		} else if nums1[i] > nums2[j] {
			g += nums2[j]
			j++
		} else {
			f = max(f, g) + nums1[i]
			g = f
			i++
			j++
		}
	}
	return max(f, g) % mod
}

TypeScript

function maxSum(nums1: number[], nums2: number[]): number {
    const mod = 1e9 + 7;
    const m = nums1.length;
    const n = nums2.length;
    let [f, g] = [0, 0];
    let [i, j] = [0, 0];
    while (i < m || j < n) {
        if (i === m) {
            g += nums2[j++];
        } else if (j === n) {
            f += nums1[i++];
        } else if (nums1[i] < nums2[j]) {
            f += nums1[i++];
        } else if (nums1[i] > nums2[j]) {
            g += nums2[j++];
        } else {
            f = g = Math.max(f, g) + nums1[i];
            i++;
            j++;
        }
    }
    return Math.max(f, g) % mod;
}