Skip to content

Latest commit

 

History

History
402 lines (345 loc) · 11.3 KB

README.md

File metadata and controls

402 lines (345 loc) · 11.3 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2529
第 212 场周赛 Q4
并查集
图
拓扑排序
数组
矩阵
排序

1632. 矩阵转换后的秩

English Version

题目描述

给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

  • 秩是从 1 开始的一个整数。
  • 如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：
    • 如果 p < q ，那么 rank(p) < rank(q)
    • 如果 p == q ，那么 rank(p) == rank(q)
    • 如果 p > q ，那么 rank(p) > rank(q)
  • 秩 需要越 小 越好。

题目保证按照上面规则 answer 数组是唯一的。

 

示例 1：

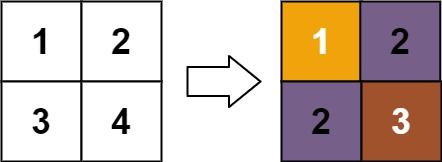
输入：matrix = [[1,2],[3,4]]
输出：[[1,2],[2,3]]
解释：
matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。
matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。

示例 2：

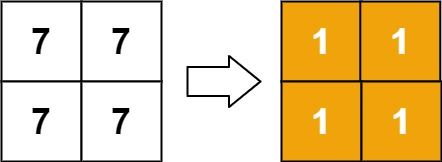
输入：matrix = [[7,7],[7,7]]
输出：[[1,1],[1,1]]

示例 3：

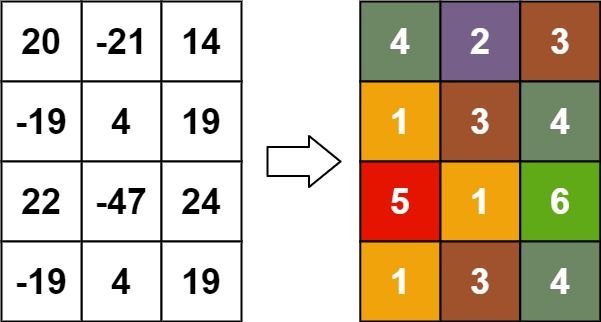
输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

 

 

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

解法

方法一：排序 + 并查集

我们先考虑简化情形：没有相同的元素。那么显然最小的元素的秩为 $1$，第二小的元素则要考虑是否和最小元素同行或同列。于是得到贪心解法：从小到大遍历元素，并维护每行、每列的最大秩，该元素的秩即为同行、同列的最大秩加 $1$。见题目：2371. 最小化网格中的最大值。

存在相同元素时则较为复杂，假设两个相同元素同行（或同列），那么就要考虑到两个元素分别对应的行（或列）的最大秩。同时还可能出现联动，比如元素 a 和 b 同行，b 和 c 同列，那么要同时考虑这三个元素。

这种联动容易想到并查集，于是我们用并查集将元素分为几个连通块，对于每个连通块，里面所有元素对应的行或列的最大秩加 $1$，即为该连通块内所有元素的秩。

时间复杂度 $O(m \times n \times \log(m \times n))$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

Python3

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            if self.size[pa] > self.size[pb]:
                self.p[pb] = pa
                self.size[pa] += self.size[pb]
            else:
                self.p[pa] = pb
                self.size[pb] += self.size[pa]

    def reset(self, x):
        self.p[x] = x
        self.size[x] = 1


class Solution:
    def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        d = defaultdict(list)
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                d[v].append((i, j))
        row_max = [0] * m
        col_max = [0] * n
        ans = [[0] * n for _ in range(m)]
        uf = UnionFind(m + n)
        for v in sorted(d):
            rank = defaultdict(int)
            for i, j in d[v]:
                uf.union(i, j + m)
            for i, j in d[v]:
                rank[uf.find(i)] = max(rank[uf.find(i)], row_max[i], col_max[j])
            for i, j in d[v]:
                ans[i][j] = row_max[i] = col_max[j] = 1 + rank[uf.find(i)]
            for i, j in d[v]:
                uf.reset(i)
                uf.reset(j + m)
        return ans

Java

class UnionFind {
    private int[] p;
    private int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public void union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }

    public void reset(int x) {
        p[x] = x;
        size[x] = 1;
    }
}

class Solution {
    public int[][] matrixRankTransform(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        TreeMap<Integer, List<int[]>> d = new TreeMap<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                d.computeIfAbsent(matrix[i][j], k -> new ArrayList<>()).add(new int[] {i, j});
            }
        }
        int[] rowMax = new int[m];
        int[] colMax = new int[n];
        int[][] ans = new int[m][n];
        UnionFind uf = new UnionFind(m + n);
        int[] rank = new int[m + n];
        for (var ps : d.values()) {
            for (var p : ps) {
                uf.union(p[0], p[1] + m);
            }
            for (var p : ps) {
                int i = p[0], j = p[1];
                rank[uf.find(i)] = Math.max(rank[uf.find(i)], Math.max(rowMax[i], colMax[j]));
            }
            for (var p : ps) {
                int i = p[0], j = p[1];
                ans[i][j] = 1 + rank[uf.find(i)];
                rowMax[i] = ans[i][j];
                colMax[j] = ans[i][j];
            }
            for (var p : ps) {
                uf.reset(p[0]);
                uf.reset(p[1] + m);
            }
        }
        return ans;
    }
}

C++

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    void unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    void reset(int x) {
        p[x] = x;
        size[x] = 1;
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        map<int, vector<pair<int, int>>> d;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                d[matrix[i][j]].push_back({i, j});
            }
        }
        vector<int> rowMax(m);
        vector<int> colMax(n);
        vector<vector<int>> ans(m, vector<int>(n));
        UnionFind uf(m + n);
        vector<int> rank(m + n);
        for (auto& [_, ps] : d) {
            for (auto& [i, j] : ps) {
                uf.unite(i, j + m);
            }
            for (auto& [i, j] : ps) {
                rank[uf.find(i)] = max({rank[uf.find(i)], rowMax[i], colMax[j]});
            }
            for (auto& [i, j] : ps) {
                ans[i][j] = rowMax[i] = colMax[j] = 1 + rank[uf.find(i)];
            }
            for (auto& [i, j] : ps) {
                uf.reset(i);
                uf.reset(j + m);
            }
        }
        return ans;
    }
};

Go

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) {
	pa, pb := uf.find(a), uf.find(b)
	if pa != pb {
		if uf.size[pa] > uf.size[pb] {
			uf.p[pb] = pa
			uf.size[pa] += uf.size[pb]
		} else {
			uf.p[pa] = pb
			uf.size[pb] += uf.size[pa]
		}
	}
}

func (uf *unionFind) reset(x int) {
	uf.p[x] = x
	uf.size[x] = 1
}

func matrixRankTransform(matrix [][]int) [][]int {
	m, n := len(matrix), len(matrix[0])
	type pair struct{ i, j int }
	d := map[int][]pair{}
	for i, row := range matrix {
		for j, v := range row {
			d[v] = append(d[v], pair{i, j})
		}
	}
	rowMax := make([]int, m)
	colMax := make([]int, n)
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
	}
	vs := []int{}
	for v := range d {
		vs = append(vs, v)
	}
	sort.Ints(vs)
	uf := newUnionFind(m + n)
	rank := make([]int, m+n)
	for _, v := range vs {
		ps := d[v]
		for _, p := range ps {
			uf.union(p.i, p.j+m)
		}
		for _, p := range ps {
			i, j := p.i, p.j
			rank[uf.find(i)] = max(rank[uf.find(i)], max(rowMax[i], colMax[j]))
		}
		for _, p := range ps {
			i, j := p.i, p.j
			ans[i][j] = 1 + rank[uf.find(i)]
			rowMax[i], colMax[j] = ans[i][j], ans[i][j]
		}
		for _, p := range ps {
			uf.reset(p.i)
			uf.reset(p.j + m)
		}
	}
	return ans
}