| comments | difficulty | edit_url | rating | source | tags | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
1897 |
第 53 场双周赛 Q3 |
|
给你一个 m x n 的整数矩阵 grid 。
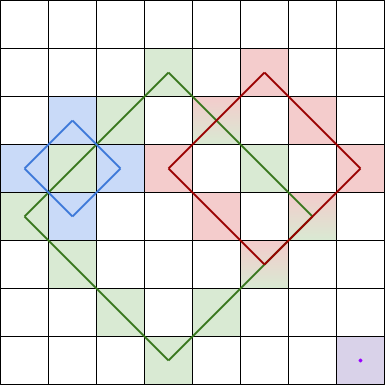
菱形和 指的是 grid 中一个正菱形 边界 上的元素之和。本题中的菱形必须为正方形旋转45度,且四个角都在一个格子当中。下图是四个可行的菱形,每个菱形和应该包含的格子都用了相应颜色标注在图中。
注意,菱形可以是一个面积为 0 的区域,如上图中右下角的紫色菱形所示。
请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和 。如果不同的和少于三个,则将它们全部返回。
示例 1:
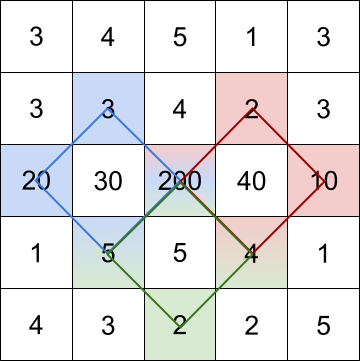
输入:grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]] 输出:[228,216,211] 解释:最大的三个菱形和如上图所示。 - 蓝色:20 + 3 + 200 + 5 = 228 - 红色:200 + 2 + 10 + 4 = 216 - 绿色:5 + 200 + 4 + 2 = 211
示例 2:
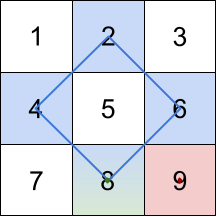
输入:grid = [[1,2,3],[4,5,6],[7,8,9]] 输出:[20,9,8] 解释:最大的三个菱形和如上图所示。 - 蓝色:4 + 2 + 6 + 8 = 20 - 红色:9 (右下角红色的面积为 0 的菱形) - 绿色:8 (下方中央面积为 0 的菱形)
示例 3:
输入:grid = [[7,7,7]] 输出:[7] 解释:所有三个可能的菱形和都相同,所以返回 [7] 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1001 <= grid[i][j] <= 105
我们可以预处理得到两个前缀和数组
接下来,我们枚举每个位置
我们将这个值加入有序集合
时间复杂度
from sortedcontainers import SortedSet
class Solution:
def getBiggestThree(self, grid: List[List[int]]) -> List[int]:
m, n = len(grid), len(grid[0])
s1 = [[0] * (n + 2) for _ in range(m + 1)]
s2 = [[0] * (n + 2) for _ in range(m + 1)]
for i, row in enumerate(grid, 1):
for j, x in enumerate(row, 1):
s1[i][j] = s1[i - 1][j - 1] + x
s2[i][j] = s2[i - 1][j + 1] + x
ss = SortedSet()
for i, row in enumerate(grid, 1):
for j, x in enumerate(row, 1):
l = min(i - 1, m - i, j - 1, n - j)
ss.add(x)
for k in range(1, l + 1):
a = s1[i + k][j] - s1[i][j - k]
b = s1[i][j + k] - s1[i - k][j]
c = s2[i][j - k] - s2[i - k][j]
d = s2[i + k][j] - s2[i][j + k]
ss.add(
a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]
)
while len(ss) > 3:
ss.remove(ss[0])
return list(ss)[::-1]class Solution {
public int[] getBiggestThree(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] s1 = new int[m + 1][n + 2];
int[][] s2 = new int[m + 1][n + 2];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1];
s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1];
}
}
TreeSet<Integer> ss = new TreeSet<>();
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int l = Math.min(Math.min(i - 1, m - i), Math.min(j - 1, n - j));
ss.add(grid[i - 1][j - 1]);
for (int k = 1; k <= l; ++k) {
int a = s1[i + k][j] - s1[i][j - k];
int b = s1[i][j + k] - s1[i - k][j];
int c = s2[i][j - k] - s2[i - k][j];
int d = s2[i + k][j] - s2[i][j + k];
ss.add(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]);
}
while (ss.size() > 3) {
ss.pollFirst();
}
}
}
int[] ans = new int[ss.size()];
for (int i = 0; i < ans.length; ++i) {
ans[i] = ss.pollLast();
}
return ans;
}
}class Solution {
public:
vector<int> getBiggestThree(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> s1(m + 1, vector<int>(n + 2));
vector<vector<int>> s2(m + 1, vector<int>(n + 2));
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1];
s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1];
}
}
set<int> ss;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int l = min({i - 1, m - i, j - 1, n - j});
ss.insert(grid[i - 1][j - 1]);
for (int k = 1; k <= l; ++k) {
int a = s1[i + k][j] - s1[i][j - k];
int b = s1[i][j + k] - s1[i - k][j];
int c = s2[i][j - k] - s2[i - k][j];
int d = s2[i + k][j] - s2[i][j + k];
ss.insert(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]);
}
while (ss.size() > 3) {
ss.erase(ss.begin());
}
}
}
return vector<int>(ss.rbegin(), ss.rend());
}
};func getBiggestThree(grid [][]int) []int {
m, n := len(grid), len(grid[0])
s1 := make([][]int, m+1)
s2 := make([][]int, m+1)
for i := range s1 {
s1[i] = make([]int, n+2)
s2[i] = make([]int, n+2)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
s1[i][j] = s1[i-1][j-1] + grid[i-1][j-1]
s2[i][j] = s2[i-1][j+1] + grid[i-1][j-1]
}
}
ss := treemap.NewWithIntComparator()
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
l := min(i-1, m-i, j-1, n-j)
ss.Put(grid[i-1][j-1], nil)
for k := 1; k <= l; k++ {
a := s1[i+k][j] - s1[i][j-k]
b := s1[i][j+k] - s1[i-k][j]
c := s2[i][j-k] - s2[i-k][j]
d := s2[i+k][j] - s2[i][j+k]
ss.Put(a+b+c+d-grid[i+k-1][j-1]+grid[i-k-1][j-1], nil)
}
for ss.Size() > 3 {
x, _ := ss.Min()
ss.Remove(x.(int))
}
}
}
ans := make([]int, ss.Size())
for i, k := range ss.Keys() {
ans[len(ans)-i-1] = k.(int)
}
return ans
}function getBiggestThree(grid: number[][]): number[] {
const m = grid.length;
const n = grid[0].length;
const s1: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0));
const s2: number[][] = Array.from({ length: m + 1 }, () => Array(n + 2).fill(0));
for (let i = 1; i <= m; ++i) {
for (let j = 1; j <= n; ++j) {
s1[i][j] = s1[i - 1][j - 1] + grid[i - 1][j - 1];
s2[i][j] = s2[i - 1][j + 1] + grid[i - 1][j - 1];
}
}
const ss = new TreeSet<number>();
for (let i = 1; i <= m; ++i) {
for (let j = 1; j <= n; ++j) {
const l = Math.min(i - 1, m - i, j - 1, n - j);
ss.add(grid[i - 1][j - 1]);
for (let k = 1; k <= l; ++k) {
const a = s1[i + k][j] - s1[i][j - k];
const b = s1[i][j + k] - s1[i - k][j];
const c = s2[i][j - k] - s2[i - k][j];
const d = s2[i + k][j] - s2[i][j + k];
ss.add(a + b + c + d - grid[i + k - 1][j - 1] + grid[i - k - 1][j - 1]);
}
while (ss.size() > 3) {
ss.shift();
}
}
}
return [...ss].reverse();
}
type Compare<T> = (lhs: T, rhs: T) => number;
class RBTreeNode<T = number> {
data: T;
count: number;
left: RBTreeNode<T> | null;
right: RBTreeNode<T> | null;
parent: RBTreeNode<T> | null;
color: number;
constructor(data: T) {
this.data = data;
this.left = this.right = this.parent = null;
this.color = 0;
this.count = 1;
}
sibling(): RBTreeNode<T> | null {
if (!this.parent) return null; // sibling null if no parent
return this.isOnLeft() ? this.parent.right : this.parent.left;
}
isOnLeft(): boolean {
return this === this.parent!.left;
}
hasRedChild(): boolean {
return (
Boolean(this.left && this.left.color === 0) ||
Boolean(this.right && this.right.color === 0)
);
}
}
class RBTree<T> {
root: RBTreeNode<T> | null;
lt: (l: T, r: T) => boolean;
constructor(compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0)) {
this.root = null;
this.lt = (l: T, r: T) => compare(l, r) < 0;
}
rotateLeft(pt: RBTreeNode<T>): void {
const right = pt.right!;
pt.right = right.left;
if (pt.right) pt.right.parent = pt;
right.parent = pt.parent;
if (!pt.parent) this.root = right;
else if (pt === pt.parent.left) pt.parent.left = right;
else pt.parent.right = right;
right.left = pt;
pt.parent = right;
}
rotateRight(pt: RBTreeNode<T>): void {
const left = pt.left!;
pt.left = left.right;
if (pt.left) pt.left.parent = pt;
left.parent = pt.parent;
if (!pt.parent) this.root = left;
else if (pt === pt.parent.left) pt.parent.left = left;
else pt.parent.right = left;
left.right = pt;
pt.parent = left;
}
swapColor(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
const tmp = p1.color;
p1.color = p2.color;
p2.color = tmp;
}
swapData(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
const tmp = p1.data;
p1.data = p2.data;
p2.data = tmp;
}
fixAfterInsert(pt: RBTreeNode<T>): void {
let parent = null;
let grandParent = null;
while (pt !== this.root && pt.color !== 1 && pt.parent?.color === 0) {
parent = pt.parent;
grandParent = pt.parent.parent;
/* Case : A
Parent of pt is left child of Grand-parent of pt */
if (parent === grandParent?.left) {
const uncle = grandParent.right;
/* Case : 1
The uncle of pt is also red
Only Recoloring required */
if (uncle && uncle.color === 0) {
grandParent.color = 0;
parent.color = 1;
uncle.color = 1;
pt = grandParent;
} else {
/* Case : 2
pt is right child of its parent
Left-rotation required */
if (pt === parent.right) {
this.rotateLeft(parent);
pt = parent;
parent = pt.parent;
}
/* Case : 3
pt is left child of its parent
Right-rotation required */
this.rotateRight(grandParent);
this.swapColor(parent!, grandParent);
pt = parent!;
}
} else {
/* Case : B
Parent of pt is right child of Grand-parent of pt */
const uncle = grandParent!.left;
/* Case : 1
The uncle of pt is also red
Only Recoloring required */
if (uncle != null && uncle.color === 0) {
grandParent!.color = 0;
parent.color = 1;
uncle.color = 1;
pt = grandParent!;
} else {
/* Case : 2
pt is left child of its parent
Right-rotation required */
if (pt === parent.left) {
this.rotateRight(parent);
pt = parent;
parent = pt.parent;
}
/* Case : 3
pt is right child of its parent
Left-rotation required */
this.rotateLeft(grandParent!);
this.swapColor(parent!, grandParent!);
pt = parent!;
}
}
}
this.root!.color = 1;
}
delete(val: T): boolean {
const node = this.find(val);
if (!node) return false;
node.count--;
if (!node.count) this.deleteNode(node);
return true;
}
deleteAll(val: T): boolean {
const node = this.find(val);
if (!node) return false;
this.deleteNode(node);
return true;
}
deleteNode(v: RBTreeNode<T>): void {
const u = BSTreplace(v);
// True when u and v are both black
const uvBlack = (u === null || u.color === 1) && v.color === 1;
const parent = v.parent!;
if (!u) {
// u is null therefore v is leaf
if (v === this.root) this.root = null;
// v is root, making root null
else {
if (uvBlack) {
// u and v both black
// v is leaf, fix double black at v
this.fixDoubleBlack(v);
} else {
// u or v is red
if (v.sibling()) {
// sibling is not null, make it red"
v.sibling()!.color = 0;
}
}
// delete v from the tree
if (v.isOnLeft()) parent.left = null;
else parent.right = null;
}
return;
}
if (!v.left || !v.right) {
// v has 1 child
if (v === this.root) {
// v is root, assign the value of u to v, and delete u
v.data = u.data;
v.left = v.right = null;
} else {
// Detach v from tree and move u up
if (v.isOnLeft()) parent.left = u;
else parent.right = u;
u.parent = parent;
if (uvBlack) this.fixDoubleBlack(u);
// u and v both black, fix double black at u
else u.color = 1; // u or v red, color u black
}
return;
}
// v has 2 children, swap data with successor and recurse
this.swapData(u, v);
this.deleteNode(u);
// find node that replaces a deleted node in BST
function BSTreplace(x: RBTreeNode<T>): RBTreeNode<T> | null {
// when node have 2 children
if (x.left && x.right) return successor(x.right);
// when leaf
if (!x.left && !x.right) return null;
// when single child
return x.left ?? x.right;
}
// find node that do not have a left child
// in the subtree of the given node
function successor(x: RBTreeNode<T>): RBTreeNode<T> {
let temp = x;
while (temp.left) temp = temp.left;
return temp;
}
}
fixDoubleBlack(x: RBTreeNode<T>): void {
if (x === this.root) return; // Reached root
const sibling = x.sibling();
const parent = x.parent!;
if (!sibling) {
// No sibiling, double black pushed up
this.fixDoubleBlack(parent);
} else {
if (sibling.color === 0) {
// Sibling red
parent.color = 0;
sibling.color = 1;
if (sibling.isOnLeft()) this.rotateRight(parent);
// left case
else this.rotateLeft(parent); // right case
this.fixDoubleBlack(x);
} else {
// Sibling black
if (sibling.hasRedChild()) {
// at least 1 red children
if (sibling.left && sibling.left.color === 0) {
if (sibling.isOnLeft()) {
// left left
sibling.left.color = sibling.color;
sibling.color = parent.color;
this.rotateRight(parent);
} else {
// right left
sibling.left.color = parent.color;
this.rotateRight(sibling);
this.rotateLeft(parent);
}
} else {
if (sibling.isOnLeft()) {
// left right
sibling.right!.color = parent.color;
this.rotateLeft(sibling);
this.rotateRight(parent);
} else {
// right right
sibling.right!.color = sibling.color;
sibling.color = parent.color;
this.rotateLeft(parent);
}
}
parent.color = 1;
} else {
// 2 black children
sibling.color = 0;
if (parent.color === 1) this.fixDoubleBlack(parent);
else parent.color = 1;
}
}
}
}
insert(data: T): boolean {
// search for a position to insert
let parent = this.root;
while (parent) {
if (this.lt(data, parent.data)) {
if (!parent.left) break;
else parent = parent.left;
} else if (this.lt(parent.data, data)) {
if (!parent.right) break;
else parent = parent.right;
} else break;
}
// insert node into parent
const node = new RBTreeNode(data);
if (!parent) this.root = node;
else if (this.lt(node.data, parent.data)) parent.left = node;
else if (this.lt(parent.data, node.data)) parent.right = node;
else {
parent.count++;
return false;
}
node.parent = parent;
this.fixAfterInsert(node);
return true;
}
find(data: T): RBTreeNode<T> | null {
let p = this.root;
while (p) {
if (this.lt(data, p.data)) {
p = p.left;
} else if (this.lt(p.data, data)) {
p = p.right;
} else break;
}
return p ?? null;
}
*inOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
if (!root) return;
for (const v of this.inOrder(root.left!)) yield v;
yield root.data;
for (const v of this.inOrder(root.right!)) yield v;
}
*reverseInOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
if (!root) return;
for (const v of this.reverseInOrder(root.right!)) yield v;
yield root.data;
for (const v of this.reverseInOrder(root.left!)) yield v;
}
}
class TreeSet<T = number> {
_size: number;
tree: RBTree<T>;
compare: Compare<T>;
constructor(
collection: T[] | Compare<T> = [],
compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0),
) {
if (typeof collection === 'function') {
compare = collection;
collection = [];
}
this._size = 0;
this.compare = compare;
this.tree = new RBTree(compare);
for (const val of collection) this.add(val);
}
size(): number {
return this._size;
}
has(val: T): boolean {
return !!this.tree.find(val);
}
add(val: T): boolean {
const successful = this.tree.insert(val);
this._size += successful ? 1 : 0;
return successful;
}
delete(val: T): boolean {
const deleted = this.tree.deleteAll(val);
this._size -= deleted ? 1 : 0;
return deleted;
}
ceil(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(p.data, val) >= 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
floor(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(val, p.data) >= 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
higher(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(val, p.data) < 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
lower(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(p.data, val) < 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
first(): T | undefined {
return this.tree.inOrder().next().value;
}
last(): T | undefined {
return this.tree.reverseInOrder().next().value;
}
shift(): T | undefined {
const first = this.first();
if (first === undefined) return undefined;
this.delete(first);
return first;
}
pop(): T | undefined {
const last = this.last();
if (last === undefined) return undefined;
this.delete(last);
return last;
}
*[Symbol.iterator](): Generator<T, void, void> {
for (const val of this.values()) yield val;
}
*keys(): Generator<T, void, void> {
for (const val of this.values()) yield val;
}
*values(): Generator<T, undefined, void> {
for (const val of this.tree.inOrder()) yield val;
return undefined;
}
/**
* Return a generator for reverse order traversing the set
*/
*rvalues(): Generator<T, undefined, void> {
for (const val of this.tree.reverseInOrder()) yield val;
return undefined;
}
}
class TreeMultiSet<T = number> {
_size: number;
tree: RBTree<T>;
compare: Compare<T>;
constructor(
collection: T[] | Compare<T> = [],
compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0),
) {
if (typeof collection === 'function') {
compare = collection;
collection = [];
}
this._size = 0;
this.compare = compare;
this.tree = new RBTree(compare);
for (const val of collection) this.add(val);
}
size(): number {
return this._size;
}
has(val: T): boolean {
return !!this.tree.find(val);
}
add(val: T): boolean {
const successful = this.tree.insert(val);
this._size++;
return successful;
}
delete(val: T): boolean {
const successful = this.tree.delete(val);
if (!successful) return false;
this._size--;
return true;
}
count(val: T): number {
const node = this.tree.find(val);
return node ? node.count : 0;
}
ceil(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(p.data, val) >= 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
floor(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(val, p.data) >= 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
higher(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(val, p.data) < 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
lower(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(p.data, val) < 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
first(): T | undefined {
return this.tree.inOrder().next().value;
}
last(): T | undefined {
return this.tree.reverseInOrder().next().value;
}
shift(): T | undefined {
const first = this.first();
if (first === undefined) return undefined;
this.delete(first);
return first;
}
pop(): T | undefined {
const last = this.last();
if (last === undefined) return undefined;
this.delete(last);
return last;
}
*[Symbol.iterator](): Generator<T, void, void> {
yield* this.values();
}
*keys(): Generator<T, void, void> {
for (const val of this.values()) yield val;
}
*values(): Generator<T, undefined, void> {
for (const val of this.tree.inOrder()) {
let count = this.count(val);
while (count--) yield val;
}
return undefined;
}
/**
* Return a generator for reverse order traversing the multi-set
*/
*rvalues(): Generator<T, undefined, void> {
for (const val of this.tree.reverseInOrder()) {
let count = this.count(val);
while (count--) yield val;
}
return undefined;
}
}