Skip to content

Latest commit

 

History

History
326 lines (285 loc) · 10.2 KB

README.md

File metadata and controls

326 lines (285 loc) · 10.2 KB
Raw
comments difficulty edit_url tags
true
困难
图
数组
矩阵

2123. 使矩阵中的 1 互不相邻的最小操作数 🔒

English Version

题目描述

给你一个 下标从 0 开始 的矩阵 grid。每次操作，你可以把 grid 中的 一个 1 变成 0 。

如果一个矩阵中，没有 1 与其它的 1 四连通（也就是说所有 1 在上下左右四个方向上不能与其他 1 相邻），那么该矩阵就是 完全独立 的。

请返回让 grid 成为 完全独立 的矩阵的 最小操作数。

 

示例 1:

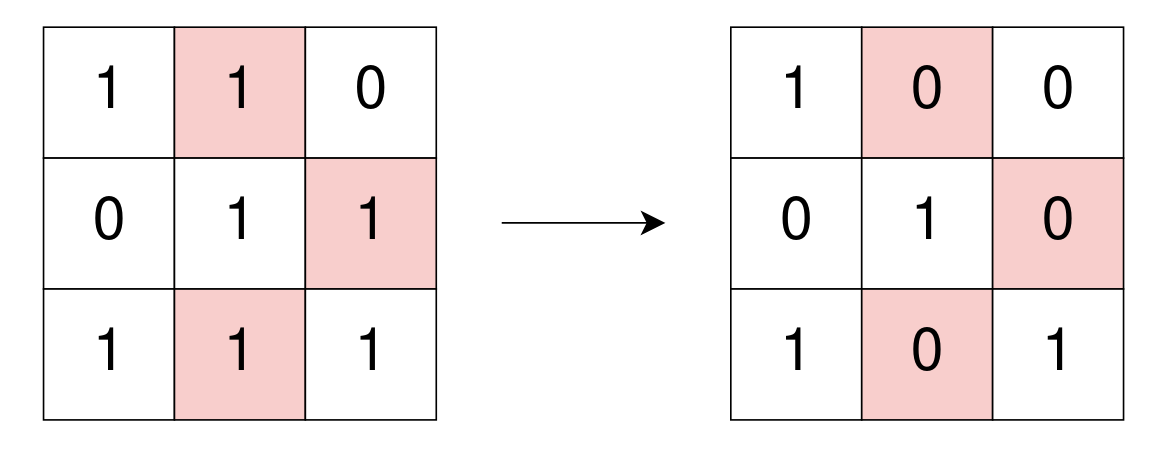
输入: grid = [[1,1,0],[0,1,1],[1,1,1]]
输出: 3
解释: 可以进行三次操作（把 grid[0][1], grid[1][2] 和 grid[2][1] 变成 0）。
操作后的矩阵中的所有的 1 与其它 1 均不相邻，因此矩阵是完全独立的。

示例 2:

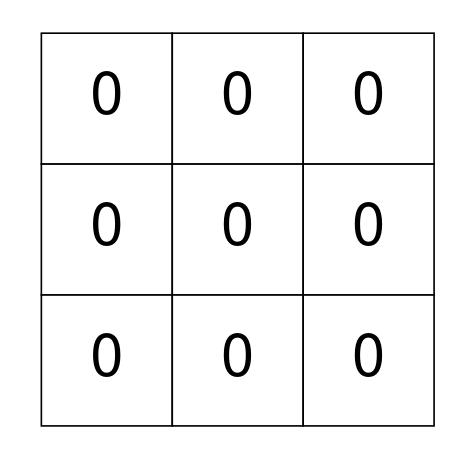
输入: grid = [[0,0,0],[0,0,0],[0,0,0]]
输出: 0
解释: 矩阵中没有 1，此时矩阵也是完全独立的，因此无需操作，返回 0。

示例 3:

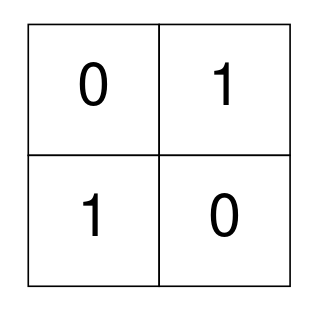
输入: grid = [[0,1],[1,0]]
输出: 0
解释: 矩阵中的所有的 1 与其它 1 均不相邻，已经是完全独立的，因此无需操作，返回 0。

 

提示:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] 是 0 或者 1.

解法

方法一：匈牙利算法

我们注意到，如果矩阵中的两个 $1$ 相邻，那么它们一定属于不同的组。因此，我们可以把矩阵中所有的 $1$ 视为点，相邻的两个 $1$ 之间连一条边，构建二分图。

那么，问题可以转化为求二分图最小点覆盖，也即选出最少数目的点来覆盖所有的边。由于二分图的最小点覆盖数等于最大匹配数，因此我们可以使用匈牙利算法求出二分图的最大匹配数。

匈牙利算法的核心思想是，不断地从未匹配的点出发，寻找增广路径，直到没有增广路径为止，就得到了最大匹配。

时间复杂度 $O(m \times n)$，其中 $n$ 和 $m$ 分别是矩阵中 $1$ 的数目以及边的数目。

Python3

class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        def find(i: int) -> int:
            for j in g[i]:
                if j not in vis:
                    vis.add(j)
                    if match[j] == -1 or find(match[j]):
                        match[j] = i
                        return 1
            return 0

        g = defaultdict(list)
        m, n = len(grid), len(grid[0])
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if (i + j) % 2 and v:
                    x = i * n + j
                    if i < m - 1 and grid[i + 1][j]:
                        g[x].append(x + n)
                    if i and grid[i - 1][j]:
                        g[x].append(x - n)
                    if j < n - 1 and grid[i][j + 1]:
                        g[x].append(x + 1)
                    if j and grid[i][j - 1]:
                        g[x].append(x - 1)

        match = [-1] * (m * n)
        ans = 0
        for i in g.keys():
            vis = set()
            ans += find(i)
        return ans

Java

class Solution {
    private Map<Integer, List<Integer>> g = new HashMap<>();
    private Set<Integer> vis = new HashSet<>();
    private int[] match;

    public int minimumOperations(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i + j) % 2 == 1 && grid[i][j] == 1) {
                    int x = i * n + j;
                    if (i < m - 1 && grid[i + 1][j] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x + n);
                    }
                    if (i > 0 && grid[i - 1][j] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x - n);
                    }
                    if (j < n - 1 && grid[i][j + 1] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x + 1);
                    }
                    if (j > 0 && grid[i][j - 1] == 1) {
                        g.computeIfAbsent(x, z -> new ArrayList<>()).add(x - 1);
                    }
                }
            }
        }
        match = new int[m * n];
        Arrays.fill(match, -1);
        int ans = 0;
        for (int i : g.keySet()) {
            ans += find(i);
            vis.clear();
        }
        return ans;
    }

    private int find(int i) {
        for (int j : g.get(i)) {
            if (vis.add(j)) {
                if (match[j] == -1 || find(match[j]) == 1) {
                    match[j] = i;
                    return 1;
                }
            }
        }
        return 0;
    }
}

C++

class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> match(m * n, -1);
        unordered_set<int> vis;
        unordered_map<int, vector<int>> g;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if ((i + j) % 2 && grid[i][j]) {
                    int x = i * n + j;
                    if (i < m - 1 && grid[i + 1][j]) {
                        g[x].push_back(x + n);
                    }
                    if (i && grid[i - 1][j]) {
                        g[x].push_back(x - n);
                    }
                    if (j < n - 1 && grid[i][j + 1]) {
                        g[x].push_back(x + 1);
                    }
                    if (j && grid[i][j - 1]) {
                        g[x].push_back(x - 1);
                    }
                }
            }
        }
        int ans = 0;
        function<int(int)> find = [&](int i) -> int {
            for (int& j : g[i]) {
                if (!vis.count(j)) {
                    vis.insert(j);
                    if (match[j] == -1 || find(match[j])) {
                        match[j] = i;
                        return 1;
                    }
                }
            }
            return 0;
        };
        for (auto& [i, _] : g) {
            ans += find(i);
            vis.clear();
        }
        return ans;
    }
};

Go

func minimumOperations(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	vis := map[int]bool{}
	match := make([]int, m*n)
	for i := range match {
		match[i] = -1
	}
	g := map[int][]int{}
	for i, row := range grid {
		for j, v := range row {
			if (i+j)&1 == 1 && v == 1 {
				x := i*n + j
				if i < m-1 && grid[i+1][j] == 1 {
					g[x] = append(g[x], x+n)
				}
				if i > 0 && grid[i-1][j] == 1 {
					g[x] = append(g[x], x-n)
				}
				if j < n-1 && grid[i][j+1] == 1 {
					g[x] = append(g[x], x+1)
				}
				if j > 0 && grid[i][j-1] == 1 {
					g[x] = append(g[x], x-1)
				}
			}
		}
	}
	var find func(int) int
	find = func(i int) int {
		for _, j := range g[i] {
			if !vis[j] {
				vis[j] = true
				if match[j] == -1 || find(match[j]) == 1 {
					match[j] = i
					return 1
				}
			}
		}
		return 0
	}
	for i := range g {
		ans += find(i)
		vis = map[int]bool{}
	}
	return
}

TypeScript

function minimumOperations(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const match: number[] = Array(m * n).fill(-1);
    const vis: Set<number> = new Set();
    const g: Map<number, number[]> = new Map();
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if ((i + j) % 2 && grid[i][j]) {
                const x = i * n + j;
                g.set(x, []);
                if (i < m - 1 && grid[i + 1][j]) {
                    g.get(x)!.push(x + n);
                }
                if (i && grid[i - 1][j]) {
                    g.get(x)!.push(x - n);
                }
                if (j < n - 1 && grid[i][j + 1]) {
                    g.get(x)!.push(x + 1);
                }
                if (j && grid[i][j - 1]) {
                    g.get(x)!.push(x - 1);
                }
            }
        }
    }
    const find = (i: number): number => {
        for (const j of g.get(i)!) {
            if (!vis.has(j)) {
                vis.add(j);
                if (match[j] === -1 || find(match[j])) {
                    match[j] = i;
                    return 1;
                }
            }
        }
        return 0;
    };
    let ans = 0;
    for (const i of g.keys()) {
        ans += find(i);
        vis.clear();
    }
    return ans;
}