Skip to content

Latest commit

 

History

History
205 lines (171 loc) · 5.53 KB

README_EN.md

File metadata and controls

205 lines (171 loc) · 5.53 KB
Raw
comments difficulty edit_url tags
true
Medium
Math
Dynamic Programming

2189. Number of Ways to Build House of Cards 🔒

中文文档

Description

You are given an integer n representing the number of playing cards you have. A house of cards meets the following conditions:

  • A house of cards consists of one or more rows of triangles and horizontal cards.
  • Triangles are created by leaning two cards against each other.
  • One card must be placed horizontally between all adjacent triangles in a row.
  • Any triangle on a row higher than the first must be placed on a horizontal card from the previous row.
  • Each triangle is placed in the leftmost available spot in the row.

Return the number of distinct house of cards you can build using all n cards. Two houses of cards are considered distinct if there exists a row where the two houses contain a different number of cards.

 

Example 1:

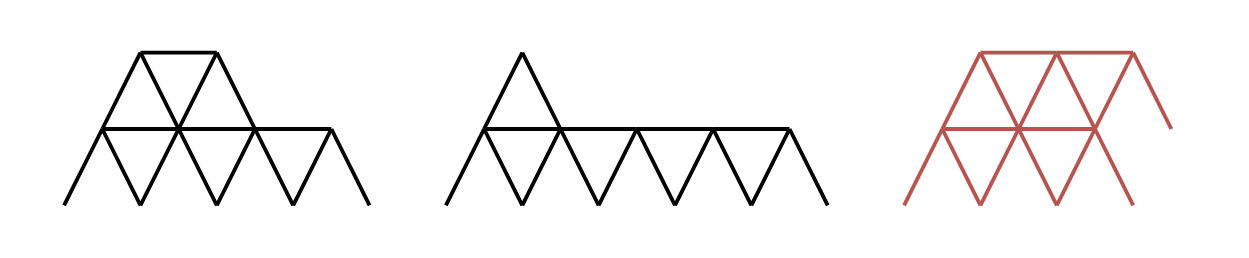
Input: n = 16
Output: 2
Explanation: The two valid houses of cards are shown.
The third house of cards in the diagram is not valid because the rightmost triangle on the top row is not placed on top of a horizontal card.

Example 2:

Input: n = 2
Output: 1
Explanation: The one valid house of cards is shown.

Example 3:

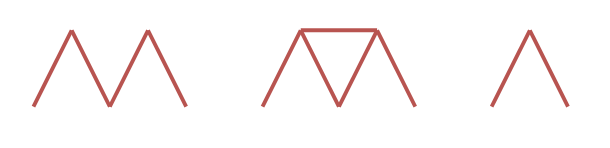
Input: n = 4
Output: 0
Explanation: The three houses of cards in the diagram are not valid.
The first house of cards needs a horizontal card placed between the two triangles.
The second house of cards uses 5 cards.
The third house of cards uses 2 cards.

 

Constraints:

  • 1 <= n <= 500

Solutions

Solution 1

Python3

class Solution:
    def houseOfCards(self, n: int) -> int:
        @cache
        def dfs(n: int, k: int) -> int:
            x = 3 * k + 2
            if x > n:
                return 0
            if x == n:
                return 1
            return dfs(n - x, k + 1) + dfs(n, k + 1)

        return dfs(n, 0)

Java

class Solution {
    private Integer[][] f;

    public int houseOfCards(int n) {
        f = new Integer[n + 1][n / 3];
        return dfs(n, 0);
    }

    private int dfs(int n, int k) {
        int x = 3 * k + 2;
        if (x > n) {
            return 0;
        }
        if (x == n) {
            return 1;
        }
        if (f[n][k] != null) {
            return f[n][k];
        }
        return f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
    }
}

C++

class Solution {
public:
    int houseOfCards(int n) {
        int f[n + 1][n / 3 + 1];
        memset(f, -1, sizeof(f));
        function<int(int, int)> dfs = [&](int n, int k) -> int {
            int x = 3 * k + 2;
            if (x > n) {
                return 0;
            }
            if (x == n) {
                return 1;
            }
            if (f[n][k] != -1) {
                return f[n][k];
            }
            return f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
        };
        return dfs(n, 0);
    }
};

Go

func houseOfCards(n int) int {
	f := make([][]int, n+1)
	for i := range f {
		f[i] = make([]int, n/3+1)
		for j := range f[i] {
			f[i][j] = -1
		}
	}
	var dfs func(n, k int) int
	dfs = func(n, k int) int {
		x := 3*k + 2
		if x > n {
			return 0
		}
		if x == n {
			return 1
		}
		if f[n][k] == -1 {
			f[n][k] = dfs(n-x, k+1) + dfs(n, k+1)
		}
		return f[n][k]
	}
	return dfs(n, 0)
}

TypeScript

function houseOfCards(n: number): number {
    const f: number[][] = Array(n + 1)
        .fill(0)
        .map(() => Array(Math.floor(n / 3) + 1).fill(-1));
    const dfs = (n: number, k: number): number => {
        const x = k * 3 + 2;
        if (x > n) {
            return 0;
        }
        if (x === n) {
            return 1;
        }
        if (f[n][k] === -1) {
            f[n][k] = dfs(n - x, k + 1) + dfs(n, k + 1);
        }
        return f[n][k];
    };
    return dfs(n, 0);
}