Skip to content

Latest commit

 

History

History
251 lines (205 loc) · 8.59 KB

README.md

File metadata and controls

251 lines (205 loc) · 8.59 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2453
第 318 场周赛 Q4
数组
动态规划
排序

2463. 最小移动总距离

English Version

题目描述

X 轴上有一些机器人和工厂。给你一个整数数组 robot ，其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ，其中 factory[j] = [positionj, limitj] ，表示第 j 个工厂的位置在 positionj ，且第 j 个工厂最多可以修理 limitj 个机器人。

每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。

所有机器人一开始都是坏的，他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向，要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时，这个工厂会维修这个机器人，且机器人停止移动。

任何时刻，你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。

请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。

注意：

  • 所有机器人移动速度相同。
  • 如果两个机器人移动方向相同，它们永远不会碰撞。
  • 如果两个机器人迎面相遇，它们也不会碰撞，它们彼此之间会擦肩而过。
  • 如果一个机器人经过了一个已经达到上限的工厂，机器人会当作工厂不存在，继续移动。
  • 机器人从位置 x 到位置 y 的移动距离为 |y - x| 。

 

示例 1：

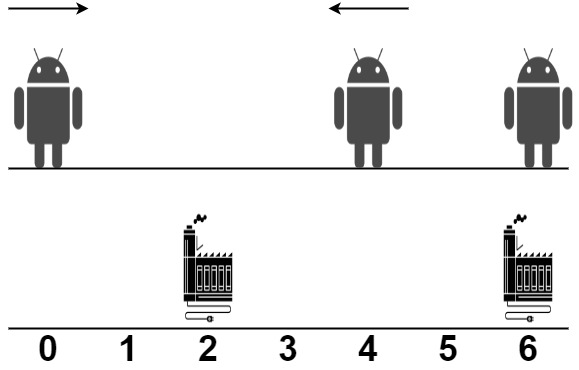
输入：robot = [0,4,6], factory = [[2,2],[6,2]]
输出：4
解释：如上图所示：
- 第一个机器人从位置 0 沿着正方向移动，在第一个工厂处维修。
- 第二个机器人从位置 4 沿着负方向移动，在第一个工厂处维修。
- 第三个机器人在位置 6 被第二个工厂维修，它不需要移动。
第一个工厂的维修上限是 2 ，它维修了 2 个机器人。
第二个工厂的维修上限是 2 ，它维修了 1 个机器人。
总移动距离是 |2 - 0| + |2 - 4| + |6 - 6| = 4 。没有办法得到比 4 更少的总移动距离。

示例 2：

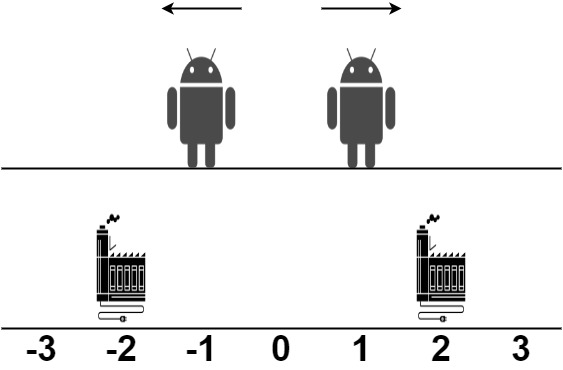
输入：robot = [1,-1], factory = [[-2,1],[2,1]]
输出：2
解释：如上图所示：
- 第一个机器人从位置 1 沿着正方向移动，在第二个工厂处维修。
- 第二个机器人在位置 -1 沿着负方向移动，在第一个工厂处维修。
第一个工厂的维修上限是 1 ，它维修了 1 个机器人。
第二个工厂的维修上限是 1 ，它维修了 1 个机器人。
总移动距离是 |2 - 1| + |(-2) - (-1)| = 2 。没有办法得到比 2 更少的总移动距离。

 

提示：

  • 1 <= robot.length, factory.length <= 100
  • factory[j].length == 2
  • -109 <= robot[i], positionj <= 109
  • 0 <= limitj <= robot.length
  • 测试数据保证所有机器人都可以被维修。

解法

方法一：记忆化搜索

我们先对机器人和工厂进行升序排列。然后定义函数 $dfs(i, j)$ 表示从第 $i$ 个机器人开始，第 $j$ 个工厂开始维修的最小总移动距离。

对于 $dfs(i, j)$，如果第 $j$ 个工厂不维修机器人，那么 $dfs(i, j)=dfs(i, j+1)$。如果第 $j$ 个工厂维修机器人，我们可以枚举第 $j$ 个工厂维修的机器人的数量，找出最小的总移动距离。即 $dfs(i, j) = min(dfs(i + k + 1, j + 1) + \sum_{t = 0}^{k} |robot[i + t] - factory[j][0|)$。

时间复杂度 $O(m^2\times n)$，空间复杂度 $O(m\times n)$。其中 $m$ 和 $n$ 分别为机器人数量和工厂数量。

Python3

class Solution:
    def minimumTotalDistance(self, robot: List[int], factory: List[List[int]]) -> int:
        @cache
        def dfs(i, j):
            if i == len(robot):
                return 0
            if j == len(factory):
                return inf
            ans = dfs(i, j + 1)
            t = 0
            for k in range(factory[j][1]):
                if i + k == len(robot):
                    break
                t += abs(robot[i + k] - factory[j][0])
                ans = min(ans, t + dfs(i + k + 1, j + 1))
            return ans

        robot.sort()
        factory.sort()
        ans = dfs(0, 0)
        dfs.cache_clear()
        return ans

Java

class Solution {
    private long[][] f;
    private List<Integer> robot;
    private int[][] factory;

    public long minimumTotalDistance(List<Integer> robot, int[][] factory) {
        Collections.sort(robot);
        Arrays.sort(factory, (a, b) -> a[0] - b[0]);
        this.robot = robot;
        this.factory = factory;
        f = new long[robot.size()][factory.length];
        return dfs(0, 0);
    }

    private long dfs(int i, int j) {
        if (i == robot.size()) {
            return 0;
        }
        if (j == factory.length) {
            return Long.MAX_VALUE / 1000;
        }
        if (f[i][j] != 0) {
            return f[i][j];
        }
        long ans = dfs(i, j + 1);
        long t = 0;
        for (int k = 0; k < factory[j][1]; ++k) {
            if (i + k == robot.size()) {
                break;
            }
            t += Math.abs(robot.get(i + k) - factory[j][0]);
            ans = Math.min(ans, t + dfs(i + k + 1, j + 1));
        }
        f[i][j] = ans;
        return ans;
    }
}

C++

using ll = long long;

class Solution {
public:
    long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
        sort(robot.begin(), robot.end());
        sort(factory.begin(), factory.end());
        vector<vector<ll>> f(robot.size(), vector<ll>(factory.size()));
        function<ll(int i, int j)> dfs = [&](int i, int j) -> ll {
            if (i == robot.size()) return 0;
            if (j == factory.size()) return 1e15;
            if (f[i][j]) return f[i][j];
            ll ans = dfs(i, j + 1);
            ll t = 0;
            for (int k = 0; k < factory[j][1]; ++k) {
                if (i + k >= robot.size()) break;
                t += abs(robot[i + k] - factory[j][0]);
                ans = min(ans, t + dfs(i + k + 1, j + 1));
            }
            f[i][j] = ans;
            return ans;
        };
        return dfs(0, 0);
    }
};

Go

func minimumTotalDistance(robot []int, factory [][]int) int64 {
	sort.Ints(robot)
	sort.Slice(factory, func(i, j int) bool { return factory[i][0] < factory[j][0] })
	f := make([][]int, len(robot))
	for i := range f {
		f[i] = make([]int, len(factory))
	}
	var dfs func(i, j int) int
	dfs = func(i, j int) int {
		if i == len(robot) {
			return 0
		}
		if j == len(factory) {
			return 1e15
		}
		if f[i][j] != 0 {
			return f[i][j]
		}
		ans := dfs(i, j+1)
		t := 0
		for k := 0; k < factory[j][1]; k++ {
			if i+k >= len(robot) {
				break
			}
			t += abs(robot[i+k] - factory[j][0])
			ans = min(ans, t+dfs(i+k+1, j+1))
		}
		f[i][j] = ans
		return ans
	}
	return int64(dfs(0, 0))
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}