Skip to content

Latest commit

 

History

History
186 lines (150 loc) · 4.82 KB

README.md

File metadata and controls

186 lines (150 loc) · 4.82 KB
Raw
comments difficulty edit_url rating source tags
true
简单
1405
第 373 场周赛 Q1
数组
数学
矩阵
模拟

2946. 循环移位后的矩阵相似检查

English Version

题目描述

给你一个下标从 0 开始且大小为 m x n 的整数矩阵 mat 和一个整数 k 。请你将矩阵中的 奇数 行循环 右 移 k 次，偶数 行循环 左 移 k 次。

如果初始矩阵和最终矩阵完全相同，则返回 true ，否则返回 false 。

 

示例 1：

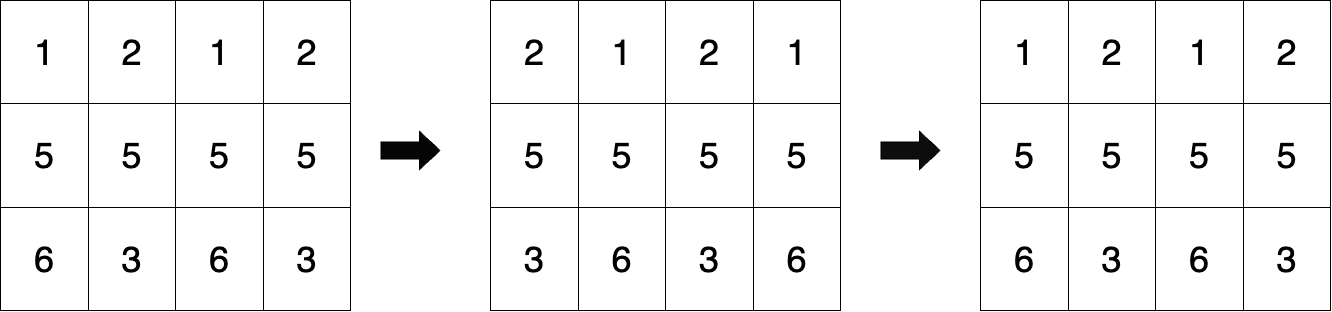
输入：mat = [[1,2,1,2],[5,5,5,5],[6,3,6,3]], k = 2
输出：true
解释：


初始矩阵如图一所示。
图二表示对奇数行右移一次且对偶数行左移一次后的矩阵状态。
图三是经过两次循环移位后的最终矩阵状态，与初始矩阵相同。
因此，返回 true 。

示例 2：

输入：mat = [[2,2],[2,2]], k = 3
输出：true
解释：由于矩阵中的所有值都相等，即使进行循环移位，矩阵仍然保持不变。因此，返回 true 。

示例 3：

输入：mat = [[1,2]], k = 1
输出：false
解释：循环移位一次后，mat = [[2,1]]，与初始矩阵不相等。因此，返回 false 。

 

提示：

  • 1 <= mat.length <= 25
  • 1 <= mat[i].length <= 25
  • 1 <= mat[i][j] <= 25
  • 1 <= k <= 50

解法

方法一

Python3

class Solution:
    def areSimilar(self, mat: List[List[int]], k: int) -> bool:
        n = len(mat[0])
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                if i % 2 == 1 and x != mat[i][(j + k) % n]:
                    return False
                if i % 2 == 0 and x != mat[i][(j - k + n) % n]:
                    return False
        return True

Java

class Solution {
    public boolean areSimilar(int[][] mat, int k) {
        int m = mat.length, n = mat[0].length;
        k %= n;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i % 2 == 1 && mat[i][j] != mat[i][(j + k) % n]) {
                    return false;
                }
                if (i % 2 == 0 && mat[i][j] != mat[i][(j - k + n) % n]) {
                    return false;
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool areSimilar(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        k %= n;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i % 2 == 1 && mat[i][j] != mat[i][(j + k) % n]) {
                    return false;
                }
                if (i % 2 == 0 && mat[i][j] != mat[i][(j - k + n) % n]) {
                    return false;
                }
            }
        }
        return true;
    }
};

Go

func areSimilar(mat [][]int, k int) bool {
	n := len(mat[0])
	k %= n
	for i, row := range mat {
		for j, x := range row {
			if i%2 == 1 && x != mat[i][(j+k)%n] {
				return false
			}
			if i%2 == 0 && x != mat[i][(j-k+n)%n] {
				return false
			}
		}
	}
	return true
}

TypeScript

function areSimilar(mat: number[][], k: number): boolean {
    const m = mat.length;
    const n = mat[0].length;
    k %= n;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (i % 2 === 1 && mat[i][j] !== mat[i][(j + k) % n]) {
                return false;
            }
            if (i % 2 === 0 && mat[i][j] !== mat[i][(j - k + n) % n]) {
                return false;
            }
        }
    }
    return true;
}