| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2270 |
第 409 场周赛 Q3 |
|
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:
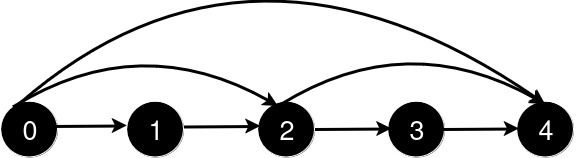
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:
新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。
新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。
新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。
示例 2:
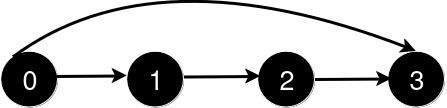
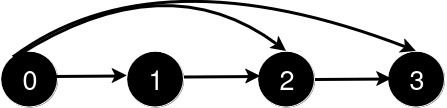
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:
新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。
新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。
提示:
3 <= n <= 1051 <= queries.length <= 105queries[i].length == 20 <= queries[i][0] < queries[i][1] < n1 < queries[i][1] - queries[i][0]- 查询中不存在重复的道路。
- 不存在两个查询都满足
i != j且queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
我们定义一个长度为
对于每次查询
在这个过程中,我们维护一个变量
时间复杂度
class Solution:
def shortestDistanceAfterQueries(
self, n: int, queries: List[List[int]]
) -> List[int]:
nxt = list(range(1, n))
ans = []
cnt = n - 1
for u, v in queries:
if 0 < nxt[u] < v:
i = nxt[u]
while i < v:
cnt -= 1
nxt[i], i = 0, nxt[i]
nxt[u] = v
ans.append(cnt)
return ansclass Solution {
public int[] shortestDistanceAfterQueries(int n, int[][] queries) {
int[] nxt = new int[n - 1];
for (int i = 1; i < n; ++i) {
nxt[i - 1] = i;
}
int m = queries.length;
int cnt = n - 1;
int[] ans = new int[m];
for (int i = 0; i < m; ++i) {
int u = queries[i][0], v = queries[i][1];
if (nxt[u] > 0 && nxt[u] < v) {
int j = nxt[u];
while (j < v) {
--cnt;
int t = nxt[j];
nxt[j] = 0;
j = t;
}
nxt[u] = v;
}
ans[i] = cnt;
}
return ans;
}
}class Solution {
public:
vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
vector<int> nxt(n - 1);
iota(nxt.begin(), nxt.end(), 1);
int cnt = n - 1;
vector<int> ans;
for (const auto& q : queries) {
int u = q[0], v = q[1];
if (nxt[u] && nxt[u] < v) {
int i = nxt[u];
while (i < v) {
--cnt;
int t = nxt[i];
nxt[i] = 0;
i = t;
}
nxt[u] = v;
}
ans.push_back(cnt);
}
return ans;
}
};func shortestDistanceAfterQueries(n int, queries [][]int) (ans []int) {
nxt := make([]int, n-1)
for i := range nxt {
nxt[i] = i + 1
}
cnt := n - 1
for _, q := range queries {
u, v := q[0], q[1]
if nxt[u] > 0 && nxt[u] < v {
i := nxt[u]
for i < v {
cnt--
nxt[i], i = 0, nxt[i]
}
nxt[u] = v
}
ans = append(ans, cnt)
}
return
}function shortestDistanceAfterQueries(n: number, queries: number[][]): number[] {
const nxt: number[] = Array.from({ length: n - 1 }, (_, i) => i + 1);
const ans: number[] = [];
let cnt = n - 1;
for (const [u, v] of queries) {
if (nxt[u] && nxt[u] < v) {
let i = nxt[u];
while (i < v) {
--cnt;
[nxt[i], i] = [0, nxt[i]];
}
nxt[u] = v;
}
ans.push(cnt);
}
return ans;
}