Skip to content

Latest commit

 

History

History
279 lines (226 loc) · 8.35 KB

README.md

File metadata and controls

279 lines (226 loc) · 8.35 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1565
第 410 场周赛 Q2
树
深度优先搜索

3249. 统计好节点的数目

English Version

题目描述

现有一棵 无向 树，树中包含 n 个节点，按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。

如果一个节点的所有子节点为根的 子树 包含的节点数相同，则认为该节点是一个 好节点。

返回给定树中 好节点 的数量。

子树 指的是一个节点以及它所有后代节点构成的一棵树。

 

 

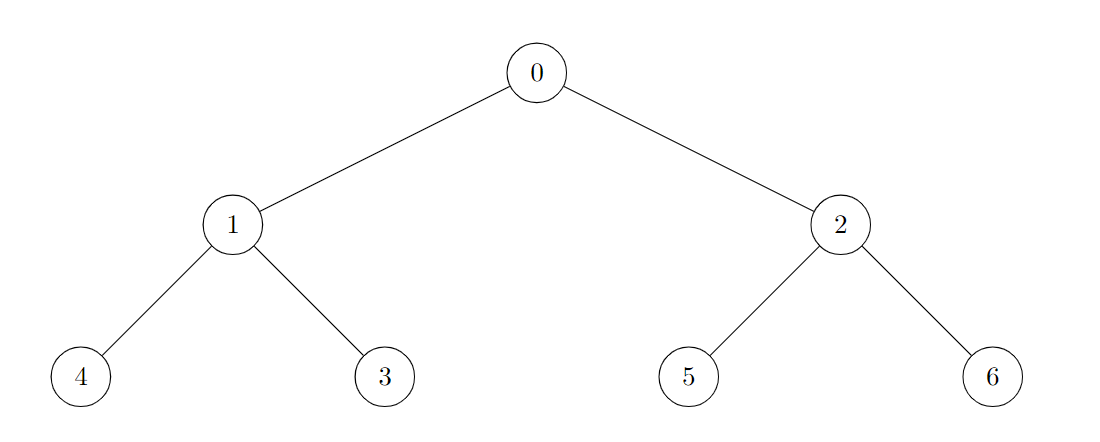
示例 1：

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

输出：7

说明：

树的所有节点都是好节点。

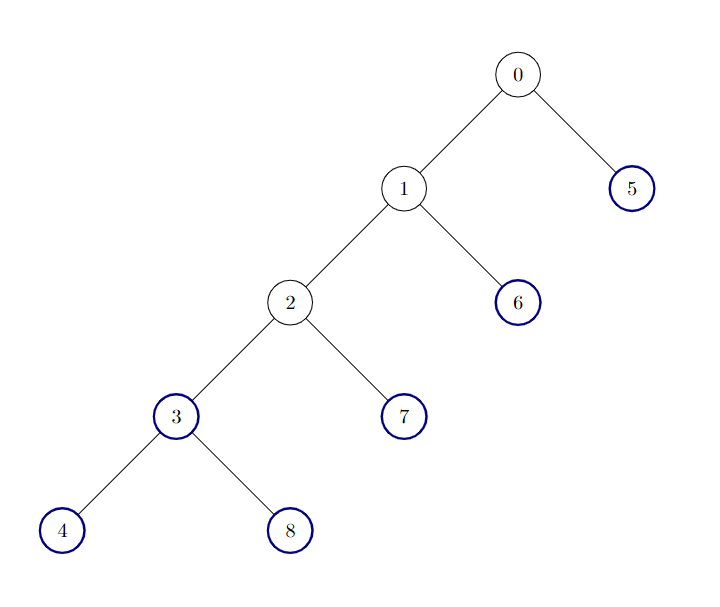
示例 2：

输入：edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

输出：6

说明：

树中有 6 个好节点。上图中已将这些节点着色。

示例 3：

输入：edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

输出：12

解释：

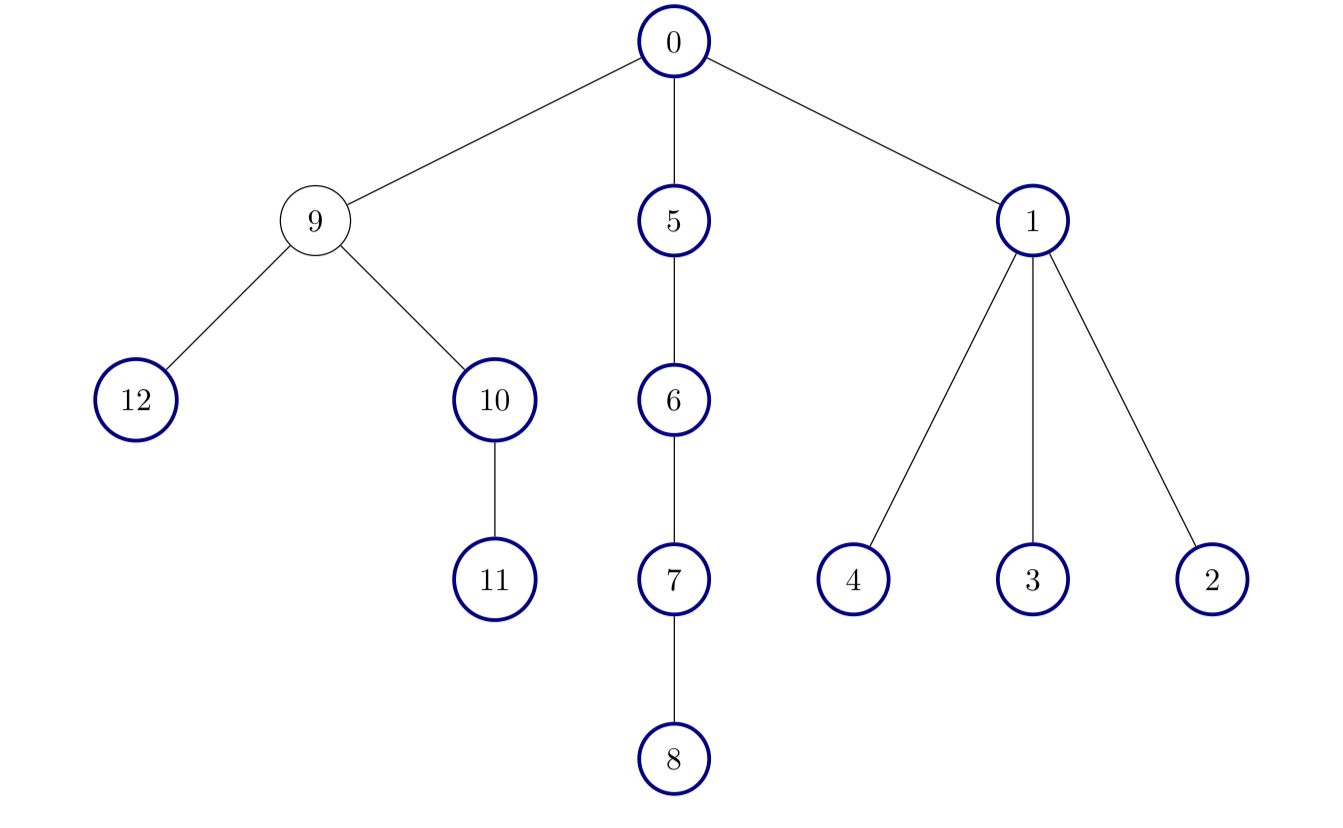
除了节点 9 以外其他所有节点都是好节点。

 

提示：

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • 输入确保 edges 总表示一棵有效的树。

解法

方法一：DFS

我们先根据题目给定的边 $\textit{edges}$ 构建出树的邻接表 $\textit{g}$，其中 $\textit{g}[a]$ 表示节点 $a$ 的所有邻居节点。

然后，我们设计一个函数 $\textit{dfs}(a, \textit{fa})$，表示计算以节点 $a$ 为根的子树中的节点数，并累计好节点的数量。其中 $\textit{fa}$ 表示节点 $a$ 的父节点。

函数 $\textit{dfs}(a, \textit{fa})$ 的执行过程如下：

  1. 初始化变量 $\textit{pre} = -1$, $\textit{cnt} = 1$, $\textit{ok} = 1$，分别表示节点 $a$ 的某个子树的节点数、节点 $a$ 的所有子树的节点数、以及节点 $a$ 是否为好节点。
  2. 遍历节点 $a$ 的所有邻居节点 $b$，如果 $b$ 不等于 $\textit{fa}$，则递归调用 $\textit{dfs}(b, a)$，返回值为 $\textit{cur}$，并累加到 $\textit{cnt}$ 中。如果 $\textit{pre} &lt; 0$，则将 $\textit{cur}$ 赋值给 $\textit{pre}$；否则，如果 $\textit{pre}$ 不等于 $\textit{cur}$，说明节点 $a$ 的不同子树的节点数不同，将 $\textit{ok}$ 置为 $0$。
  3. 最后，累加 $\textit{ok}$ 到答案中，并返回 $\textit{cnt}$。

在主函数中，我们调用 $\textit{dfs}(0, -1)$，最后返回答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 表示节点的数量。

Python3

class Solution:
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        def dfs(a: int, fa: int) -> int:
            pre = -1
            cnt = ok = 1
            for b in g[a]:
                if b != fa:
                    cur = dfs(b, a)
                    cnt += cur
                    if pre < 0:
                        pre = cur
                    elif pre != cur:
                        ok = 0
            nonlocal ans
            ans += ok
            return cnt

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        dfs(0, -1)
        return ans

Java

class Solution {
    private int ans;
    private List<Integer>[] g;

    public int countGoodNodes(int[][] edges) {
        int n = edges.length + 1;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private int dfs(int a, int fa) {
        int pre = -1, cnt = 1, ok = 1;
        for (int b : g[a]) {
            if (b != fa) {
                int cur = dfs(b, a);
                cnt += cur;
                if (pre < 0) {
                    pre = cur;
                } else if (pre != cur) {
                    ok = 0;
                }
            }
        }
        ans += ok;
        return cnt;
    }
}

C++

class Solution {
public:
    int countGoodNodes(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<int> g[n];
        for (const auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0;
        auto dfs = [&](this auto&& dfs, int a, int fa) -> int {
            int pre = -1, cnt = 1, ok = 1;
            for (int b : g[a]) {
                if (b != fa) {
                    int cur = dfs(b, a);
                    cnt += cur;
                    if (pre < 0) {
                        pre = cur;
                    } else if (pre != cur) {
                        ok = 0;
                    }
                }
            }
            ans += ok;
            return cnt;
        };
        dfs(0, -1);
        return ans;
    }
};

Go

func countGoodNodes(edges [][]int) (ans int) {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int, int) int
	dfs = func(a, fa int) int {
		pre, cnt, ok := -1, 1, 1
		for _, b := range g[a] {
			if b != fa {
				cur := dfs(b, a)
				cnt += cur
				if pre < 0 {
					pre = cur
				} else if pre != cur {
					ok = 0
				}
			}
		}
		ans += ok
		return cnt
	}
	dfs(0, -1)
	return
}

TypeScript

function countGoodNodes(edges: number[][]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    let ans = 0;
    const dfs = (a: number, fa: number): number => {
        let [pre, cnt, ok] = [-1, 1, 1];
        for (const b of g[a]) {
            if (b !== fa) {
                const cur = dfs(b, a);
                cnt += cur;
                if (pre < 0) {
                    pre = cur;
                } else if (pre !== cur) {
                    ok = 0;
                }
            }
        }
        ans += ok;
        return cnt;
    };
    dfs(0, -1);
    return ans;
}