| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1752 |
Biweekly Contest 5 Q3 |
|
There are n cities labeled from 1 to n. You are given the integer n and an array connections where connections[i] = [xi, yi, costi] indicates that the cost of connecting city xi and city yi (bidirectional connection) is costi.
Return the minimum cost to connect all the n cities such that there is at least one path between each pair of cities. If it is impossible to connect all the n cities, return -1,
The cost is the sum of the connections' costs used.
Example 1:
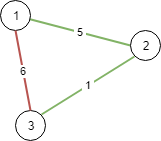
Input: n = 3, connections = [[1,2,5],[1,3,6],[2,3,1]] Output: 6 Explanation: Choosing any 2 edges will connect all cities so we choose the minimum 2.
Example 2:
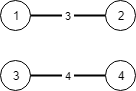
Input: n = 4, connections = [[1,2,3],[3,4,4]] Output: -1 Explanation: There is no way to connect all cities even if all edges are used.
Constraints:
1 <= n <= 1041 <= connections.length <= 104connections[i].length == 31 <= xi, yi <= nxi != yi0 <= costi <= 105
Kruskal's algorithm is a greedy algorithm used to compute the minimum spanning tree.
The basic idea of Kruskal's algorithm is to select the smallest edge from the edge set each time. If the two vertices connected by this edge are not in the same connected component, then add this edge to the minimum spanning tree, otherwise discard this edge.
For this problem, we can sort the edges in ascending order of connection cost, use a union-find set to maintain connected components, select the smallest edge each time, and if the two vertices connected by this edge are not in the same connected component, then merge these two vertices and accumulate the connection cost. If a situation occurs where the number of connected components is
The time complexity is
class Solution:
def minimumCost(self, n: int, connections: List[List[int]]) -> int:
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
connections.sort(key=lambda x: x[2])
p = list(range(n))
ans = 0
for x, y, cost in connections:
x, y = x - 1, y - 1
if find(x) == find(y):
continue
p[find(x)] = find(y)
ans += cost
n -= 1
if n == 1:
return ans
return -1class Solution {
private int[] p;
public int minimumCost(int n, int[][] connections) {
Arrays.sort(connections, Comparator.comparingInt(a -> a[2]));
p = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
}
int ans = 0;
for (int[] e : connections) {
int x = e[0] - 1, y = e[1] - 1, cost = e[2];
if (find(x) == find(y)) {
continue;
}
p[find(x)] = find(y);
ans += cost;
if (--n == 1) {
return ans;
}
}
return -1;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class Solution {
public:
int minimumCost(int n, vector<vector<int>>& connections) {
vector<int> p(n);
iota(p.begin(), p.end(), 0);
sort(connections.begin(), connections.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
int ans = 0;
function<int(int)> find = [&](int x) -> int {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
};
for (auto& e : connections) {
int x = e[0] - 1, y = e[1] - 1, cost = e[2];
if (find(x) == find(y)) {
continue;
}
p[find(x)] = find(y);
ans += cost;
if (--n == 1) {
return ans;
}
}
return -1;
}
};func minimumCost(n int, connections [][]int) (ans int) {
p := make([]int, n)
for i := range p {
p[i] = i
}
sort.Slice(connections, func(i, j int) bool { return connections[i][2] < connections[j][2] })
var find func(int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
for _, e := range connections {
x, y, cost := e[0]-1, e[1]-1, e[2]
if find(x) == find(y) {
continue
}
p[find(x)] = find(y)
ans += cost
n--
if n == 1 {
return
}
}
return -1
}function minimumCost(n: number, connections: number[][]): number {
const p: number[] = Array.from({ length: n }, (_, i) => i);
const find = (x: number): number => {
if (p[x] !== x) {
p[x] = find(p[x]);
}
return p[x];
};
connections.sort((a, b) => a[2] - b[2]);
let ans = 0;
for (const [x, y, cost] of connections) {
if (find(x - 1) === find(y - 1)) {
continue;
}
p[find(x - 1)] = find(y - 1);
ans += cost;
if (--n === 1) {
return ans;
}
}
return -1;
}