Machine Learning in No Limit Texas Holdem
t = Table(smallBlind=1, bigBlind=2, maxBuyIn=200)
for i in range(6):
r = GradientBoostingRegressor()
name = 'Player ' + str(i+1)
p = BasicPlayer(name=name, reg=r, bankroll=10**6, nRaises=10, rFactor=.7, memory=10**5)
t.addPlayer(p)
simulate(t, nHands=10000, firstTrain=2000, nTrain=1000, nBuyIn=10)
simulate(t, nHands=20, nBuyIn=10, vocal=True)['3h', 'Kc', '5c']
Player 4 checks.
Player 2 raises 270 to 270
Player 4 all-in calls with 46
224 uncalled chips return to Player 2
['3h', 'Kc', '5c', 'Qd']
['3h', 'Kc', '5c', 'Qd', '8s']
Player 2 wins 118 from main pot
This is a small library which allows for the simulation of No Limit Texas Holdem between autonomous players which are built around machine learning models. poker-learn is made specifically for use with the scikit-learn machine learning library, although any regressor which implements 'fit' and 'predict' methods will work. Fundamentally, this library consists of the Table object simulating a hand by sending GameState objects and requesting actions from its Player objects. Before the first round of learning, Players choose a random action. Several demo files are included.
sklearn - library which implements machine learning models
numpy - array manipulation library, dependency for sklearn
deuces - package which evaluates rank of poker hands, included in this project
matplotlib - graphing library, necessary for running demo
Some simplifications are made. For example, the set of all possible raises is reduced to a smaller set. This decreases the number of actions for which a Player must predict return and, as a result, decreases computational load. Specific raise amounts are chosen to represent an exponential distribution over a Player's stack. The intuition behind this decision is that a player becomes exponentially less likely to choose a raise amount as the amount increases. In addition, Players play with integer amounts of chips of uniform value, and there is no distinction made between betting and raising.
Most interestingly, Players attempt to maximize the expected value of the return on any particular action. The preferred alternative would be that Players maximize their own expected utility. That is, that the Players are risk-averse. Because risk-aversion has not been implemented, Players are prone to taking wildly large bets. I plan to address this in the future. Finally, some of the more intricate Holdem rules are excluded.
Each time a Player receives a GameState object, the Player generates a set of features corresponding to that GameState and and the action the Player has chosen. These features are stored and later associated with a label. The label is calculated at the end of each hand and is the difference between the Player's stack at the end of the hand and the Player stack size at the moment of the action. Players are intended to be sub-classed with '_genGameFeatures' and '_genActionFeatures' implemented in the sub-class, so that custom features can be generated. A BasicPlayer subclass is included in 'templates.py'. At present, features generated by BasicPlayer are very simplistic. They include the number and suit of hole cards and community cards and the Player's stack. Categorical features are represented with a binary encoding.
After each iteration, the Player is trained using a fixed amount of features and labels. The remainder of features and labels from the beginning of the Player's career are discarded. The reason for discarding is that the expected return of a Player's action is a function of the Player's future actions in any hand, so older samples become inaccurate as a Player evolves. A machine learning regressor is used to approximate a function from the set of stored features to the set of stored labels. In order to predict the best action, the Player evaluates this function for its received GameState and over the entire set of possible actions. The action which is evaluated to the maximum expected value of return is chosen.
Before Player's have been trained, they take random actions with the purpose of gathering features and labels associated with random game states. I have observed that when this period contains few hands, when Players do not sufficiently explore the state space, it can lead to some strange and upredictable behavior.
After experimenting with various machine learning models, I have had most success with linear and ensemble models. I suspect that this is because both are resistant to overfitting given the large amount of randomness that is present in poker. Ensemble models work by fitting regressors to multiple random subsets of the training data. In this way, they minimize overfitting while linear models avoid overfitting via their simplicity. Ensemble methods seem to outperform linear methods. This is likely because ensemble methods can capture the nonlinearities present in Holdem with regressors like decision trees. As for specific models, best performance was observed with GradientBoostingRegressor after brief experimentation. Linear models performed well and quickly, and support vector machines took far too long to train.
In the simplest case, Players are trained, and then test hands are narrated:
narration_demo.py
t = Table(smallBlind=1, bigBlind=2, maxBuyIn=200)
Players = []
for i in range(6):
#create BasicPlayer that uses GradientBoostingRegressor as machine learning model
#with wealth of 1 million and 10 discrete choices for raising,
#with each raise choice .7 times the next largest raise choice
#Player forgets training samples older than 100,000
r = GradientBoostingRegressor()
name = 'Player ' + str(i+1)
p = BasicPlayer(name=name, reg=r, bankroll=10**6, nRaises=10, rFactor=.7, memory=10**5)
Players.append(p)
for p in Players: t.addPlayer(p)
#simulate 'nHands' hands
#begin training after 'firstTrain' hands
#before which Players take random actions and explore state space
#Players train every 'nTrain' hands after 'firstTrain'
#Players cash out/ buy in every 'nBuyIn' hands
#table narrates each hands if 'vocal' is True
simulate(t, nHands=10000, firstTrain=2000, nTrain=1000, nBuyIn=10)
simulate(t, nHands=20, nBuyIn=10, vocal=True)Hand 5
Player 2(1141) dealt 8d and Qs
Player 4(59) dealt 6c and As
Player 2 posts small blind of 1
Player 4 posts big blind of 2
Player 2 calls 1
Player 4 raises 11 to 13
Player 2 calls 11
['3h', 'Kc', '5c']
Player 4 checks.
Player 2 raises 270 to 270
Player 4 all-in calls with 46
224 uncalled chips return to Player 2
['3h', 'Kc', '5c', 'Qd']
['3h', 'Kc', '5c', 'Qd', '8s']
Player 2 wins 118 from main pot
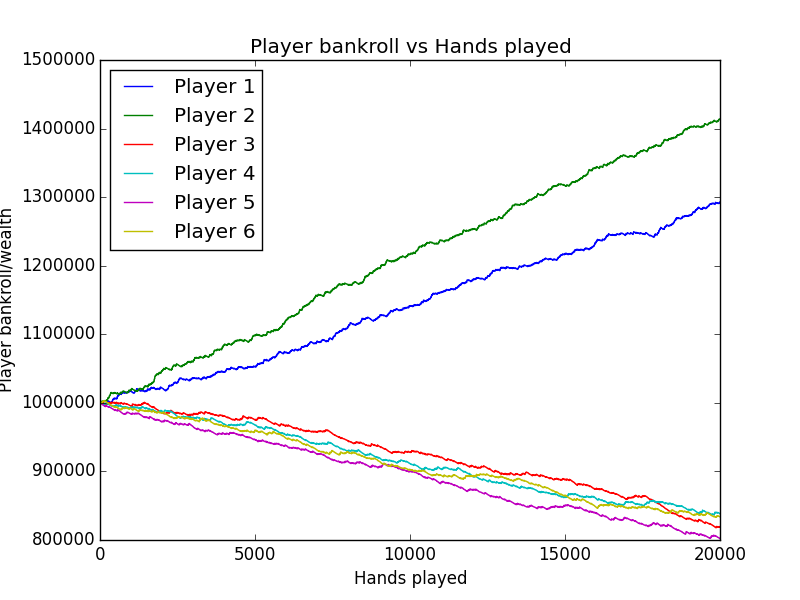
Players that are trained more have a tendency to be more skilled:
bankroll_demo.py
#train Player 1 for 1000 hands, training once
Players[0].startTraining()
simulate(t, nHands=1000, nTrain=1000, nBuyIn=10)
Players[0].stopTraining()
#train Player 2 for 10000 hands, training every 1000 hands
Players[1].startTraining()
simulate(t, nHands=10000, nTrain=1000, nBuyIn=10)
Players[1].stopTraining()
for p in Players: p.setBankroll(10**6)
#simulate 20,000 hands and save bankroll history
bankrolls = simulate(t, nHands=20000, nTrain=0, nBuyIn=10)
#plot bankroll history of each Player
for i in range(6):
bankroll = bankrolls[i]
plt.plot(range(len(bankroll)), bankroll, label=Players[i].getName())
plt.legend(loc='upper left')
plt.show()Player 2's bankroll reflects that it has trained over 10,000 more hands than Player 1.
For the purpose of testing different regressors, a demo file is included which cross-validates several regressors with features and labels taken from Players.
cross_val_demo.py
#simulate 1,000 hands, cashing out/buying in every 10 hands, without training or narrating
simulate(t, nHands=1000, nBuyIn=10, nTrain=0, vocal=False)
features = []
labels = []
for p in Players:
features.extend(p.getFeatures())
labels.extend(p.getLabels())
features = np.array(features)
labels = np.array(labels)
#shuffle features/labels
index = np.arange(len(labels))
np.random.shuffle(index)
features = features[index]
labels = labels[index]
#initialize regressors with default parameters
regressors = {LinearRegression(): 'LinearRegression',
Lasso(): 'Lasso',
RandomForestRegressor(): 'RandomForestRegressor',
GradientBoostingRegressor(): 'GradientBoostingRegressor'}
for r in regressors:
print 'Cross-validating ' + regressors[r] + '...'
print 'Rsquared:', np.mean(cross_val_score(r, features, labels))
printCross-validating Lasso...
Rsquared: 0.0902855241301
Cross-validating GradientBoostingRegressor...
Rsquared: 0.118021710842
Cross-validating LinearRegression...
Rsquared: 0.0776244830381
Cross-validating RandomForestRegressor...
Rsquared: 0.0506318142366
The MIT License (MIT)
Copyright (c) 2015 Chase M Bowers
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.