Skip to content

Latest commit

 

History

History
209 lines (160 loc) · 5.79 KB

README.md

File metadata and controls

209 lines (160 loc) · 5.79 KB
Raw
comments difficulty edit_url rating source tags
true
简单
1234
第 153 场周赛 Q1
数组

1184. 公交站间的距离

English Version

题目描述

环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

 

示例 1：

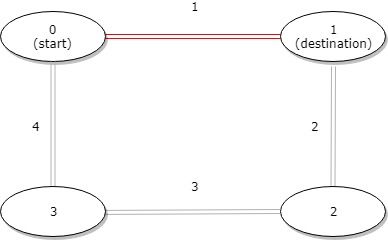
输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

 

示例 2：

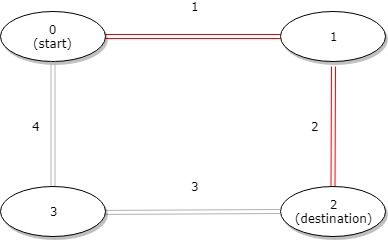
输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

 

示例 3：

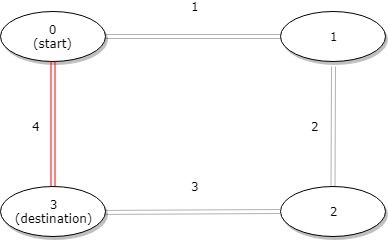
输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

 

提示：

  • 1 <= n <= 10^4
  • distance.length == n
  • 0 <= start, destination < n
  • 0 <= distance[i] <= 10^4

解法

方法一：模拟

我们可以先统计出公交车的总行驶距离 $s$，然后模拟公交车的行驶过程，从出发点开始，每次向右移动一站，直到到达目的地为止，记录下这个过程中的行驶距离 $t$，最后返回 $t$ 和 $s - t$ 中的最小值即可。

时间复杂度 $O(n)$，其中 $n$ 是数组 $\textit{distance}$ 的长度。空间复杂度 $O(1)$。

Python3

class Solution:
    def distanceBetweenBusStops(
        self, distance: List[int], start: int, destination: int
    ) -> int:
        s = sum(distance)
        t, n = 0, len(distance)
        while start != destination:
            t += distance[start]
            start = (start + 1) % n
        return min(t, s - t)

Java

class Solution {
    public int distanceBetweenBusStops(int[] distance, int start, int destination) {
        int s = Arrays.stream(distance).sum();
        int n = distance.length, t = 0;
        while (start != destination) {
            t += distance[start];
            start = (start + 1) % n;
        }
        return Math.min(t, s - t);
    }
}

C++

class Solution {
public:
    int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
        int s = accumulate(distance.begin(), distance.end(), 0);
        int t = 0, n = distance.size();
        while (start != destination) {
            t += distance[start];
            start = (start + 1) % n;
        }
        return min(t, s - t);
    }
};

Go

func distanceBetweenBusStops(distance []int, start int, destination int) int {
	s, t := 0, 0
	for _, x := range distance {
		s += x
	}
	for start != destination {
		t += distance[start]
		start = (start + 1) % len(distance)
	}
	return min(t, s-t)
}

TypeScript

function distanceBetweenBusStops(distance: number[], start: number, destination: number): number {
    const s = distance.reduce((a, b) => a + b, 0);
    const n = distance.length;
    let t = 0;
    while (start !== destination) {
        t += distance[start];
        start = (start + 1) % n;
    }
    return Math.min(t, s - t);
}

Rust

impl Solution {
    pub fn distance_between_bus_stops(distance: Vec<i32>, start: i32, destination: i32) -> i32 {
        let s: i32 = distance.iter().sum();
        let mut t = 0;
        let n = distance.len();
        let mut start = start as usize;
        let destination = destination as usize;

        while start != destination {
            t += distance[start];
            start = (start + 1) % n;
        }

        t.min(s - t)
    }
}

JavaScript

/**
 * @param {number[]} distance
 * @param {number} start
 * @param {number} destination
 * @return {number}
 */
var distanceBetweenBusStops = function (distance, start, destination) {
    const s = distance.reduce((a, b) => a + b, 0);
    const n = distance.length;
    let t = 0;
    while (start !== destination) {
        t += distance[start];
        start = (start + 1) % n;
    }
    return Math.min(t, s - t);
};