README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/1100-1199/1184.Distance%20Between%20Bus%20Stops/README_EN.md	1234	Weekly Contest 153 Q1	Array

1184. Distance Between Bus Stops

中文文档

Description

A bus has n stops numbered from 0 to n - 1 that form a circle. We know the distance between all pairs of neighboring stops where distance[i] is the distance between the stops number i and (i + 1) % n.

The bus goes along both directions i.e. clockwise and counterclockwise.

Return the shortest distance between the given start and destination stops.

 

Example 1:

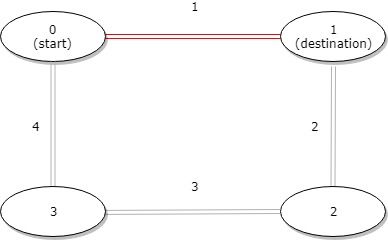
Input: distance = [1,2,3,4], start = 0, destination = 1

Output: 1

Explanation: Distance between 0 and 1 is 1 or 9, minimum is 1.

 

Example 2:

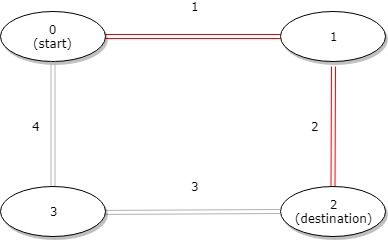
Input: distance = [1,2,3,4], start = 0, destination = 2

Output: 3

Explanation: Distance between 0 and 2 is 3 or 7, minimum is 3.

 

Example 3:

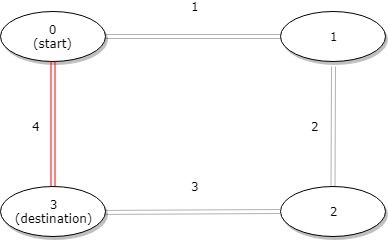
Input: distance = [1,2,3,4], start = 0, destination = 3

Output: 4

Explanation: Distance between 0 and 3 is 6 or 4, minimum is 4.

 

Constraints:

<li><code>1 &lt;= n&nbsp;&lt;= 10^4</code></li>

<li><code>distance.length == n</code></li>

<li><code>0 &lt;= start, destination &lt; n</code></li>

<li><code>0 &lt;= distance[i] &lt;= 10^4</code></li>

Solutions

Solution 1: Simulation

We can first calculate the total distance $s$ that the bus travels, then simulate the bus's journey. Starting from the departure point, we move one stop to the right each time until we reach the destination, recording the travel distance $t$ during this process. Finally, we return the minimum value between $t$ and $s - t$.

The time complexity is $O(n)$, where $n$ is the length of the array $\textit{distance}$. The space complexity is $O(1)$.

Python3

class Solution:
    def distanceBetweenBusStops(
        self, distance: List[int], start: int, destination: int
    ) -> int:
        s = sum(distance)
        t, n = 0, len(distance)
        while start != destination:
            t += distance[start]
            start = (start + 1) % n
        return min(t, s - t)

Java

class Solution {
    public int distanceBetweenBusStops(int[] distance, int start, int destination) {
        int s = Arrays.stream(distance).sum();
        int n = distance.length, t = 0;
        while (start != destination) {
            t += distance[start];
            start = (start + 1) % n;
        }
        return Math.min(t, s - t);
    }
}

C++

class Solution {
public:
    int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
        int s = accumulate(distance.begin(), distance.end(), 0);
        int t = 0, n = distance.size();
        while (start != destination) {
            t += distance[start];
            start = (start + 1) % n;
        }
        return min(t, s - t);
    }
};

Go

func distanceBetweenBusStops(distance []int, start int, destination int) int {
	s, t := 0, 0
	for _, x := range distance {
		s += x
	}
	for start != destination {
		t += distance[start]
		start = (start + 1) % len(distance)
	}
	return min(t, s-t)
}

TypeScript

function distanceBetweenBusStops(distance: number[], start: number, destination: number): number {
    const s = distance.reduce((a, b) => a + b, 0);
    const n = distance.length;
    let t = 0;
    while (start !== destination) {
        t += distance[start];
        start = (start + 1) % n;
    }
    return Math.min(t, s - t);
}

Rust

impl Solution {
    pub fn distance_between_bus_stops(distance: Vec<i32>, start: i32, destination: i32) -> i32 {
        let s: i32 = distance.iter().sum();
        let mut t = 0;
        let n = distance.len();
        let mut start = start as usize;
        let destination = destination as usize;

        while start != destination {
            t += distance[start];
            start = (start + 1) % n;
        }

        t.min(s - t)
    }
}

JavaScript

/**
 * @param {number[]} distance
 * @param {number} start
 * @param {number} destination
 * @return {number}
 */
var distanceBetweenBusStops = function (distance, start, destination) {
    const s = distance.reduce((a, b) => a + b, 0);
    const n = distance.length;
    let t = 0;
    while (start !== destination) {
        t += distance[start];
        start = (start + 1) % n;
    }
    return Math.min(t, s - t);
};