Skip to content

Latest commit

 

History

History
237 lines (189 loc) · 6.97 KB

README.md

File metadata and controls

237 lines (189 loc) · 6.97 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1561
第 179 场周赛 Q3
树
深度优先搜索
广度优先搜索

1376. 通知所有员工所需的时间

English Version

题目描述

公司里有 n 名员工，每个员工的 ID 都是独一无二的，编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。

在 manager 数组中，每个员工都有一个直属负责人，其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人，manager[headID] = -1。题目保证从属关系可以用树结构显示。

公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们，然后由这些下属通知他们的下属，直到所有的员工都得知这条紧急消息。

第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属（也就是说在 informTime[i] 分钟后，他的所有直属下属都可以开始传播这一消息）。

返回通知所有员工这一紧急消息所需要的 分钟数 。

 

示例 1：

输入：n = 1, headID = 0, manager = [-1], informTime = [0]
输出：0
解释：公司总负责人是该公司的唯一一名员工。

示例 2：

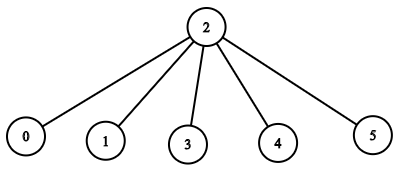
输入：n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
输出：1
解释：id = 2 的员工是公司的总负责人，也是其他所有员工的直属负责人，他需要 1 分钟来通知所有员工。
上图显示了公司员工的树结构。

 

提示：

  • 1 <= n <= 10^5
  • 0 <= headID < n
  • manager.length == n
  • 0 <= manager[i] < n
  • manager[headID] == -1
  • informTime.length == n
  • 0 <= informTime[i] <= 1000
  • 如果员工 i 没有下属，informTime[i] == 0 。
  • 题目 保证 所有员工都可以收到通知。

解法

方法一：DFS

我们先根据 $manager$ 数组构建邻接表 $g$，其中 $g[i]$ 表示员工 $i$ 的所有直接下属。

接下来，我们设计一个函数 $dfs(i)$，表示从员工 $i$ 开始，将消息通知给他的所有下属（包括直接下属、间接下属）所需要的时间，那么答案就是 $dfs(headID)$。

在函数 $dfs(i)$ 中，我们需要遍历 $i$ 的所有直接下属 $j$，对于每个下属，员工 $i$ 需要将消息通知给他，这需要花费 $informTime[i]$ 的时间，而他的所有下属需要将消息通知给他们的下属，这需要花费 $dfs(j)$ 的时间，取 $informTime[i] + dfs(j)$ 的最大值作为函数 $dfs(i)$ 的返回值即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为员工数量。

Python3

class Solution:
    def numOfMinutes(
        self, n: int, headID: int, manager: List[int], informTime: List[int]
    ) -> int:
        def dfs(i: int) -> int:
            ans = 0
            for j in g[i]:
                ans = max(ans, dfs(j) + informTime[i])
            return ans

        g = defaultdict(list)
        for i, x in enumerate(manager):
            g[x].append(i)
        return dfs(headID)

Java

class Solution {
    private List<Integer>[] g;
    private int[] informTime;

    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        this.informTime = informTime;
        for (int i = 0; i < n; ++i) {
            if (manager[i] >= 0) {
                g[manager[i]].add(i);
            }
        }
        return dfs(headID);
    }

    private int dfs(int i) {
        int ans = 0;
        for (int j : g[i]) {
            ans = Math.max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        vector<vector<int>> g(n);
        for (int i = 0; i < n; ++i) {
            if (manager[i] >= 0) {
                g[manager[i]].push_back(i);
            }
        }
        function<int(int)> dfs = [&](int i) -> int {
            int ans = 0;
            for (int j : g[i]) {
                ans = max(ans, dfs(j) + informTime[i]);
            }
            return ans;
        };
        return dfs(headID);
    }
};

Go

func numOfMinutes(n int, headID int, manager []int, informTime []int) int {
	g := make([][]int, n)
	for i, x := range manager {
		if x != -1 {
			g[x] = append(g[x], i)
		}
	}
	var dfs func(int) int
	dfs = func(i int) (ans int) {
		for _, j := range g[i] {
			ans = max(ans, dfs(j)+informTime[i])
		}
		return
	}
	return dfs(headID)
}

TypeScript

function numOfMinutes(n: number, headID: number, manager: number[], informTime: number[]): number {
    const g: number[][] = new Array(n).fill(0).map(() => []);
    for (let i = 0; i < n; ++i) {
        if (manager[i] !== -1) {
            g[manager[i]].push(i);
        }
    }
    const dfs = (i: number): number => {
        let ans = 0;
        for (const j of g[i]) {
            ans = Math.max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    };
    return dfs(headID);
}

C#

public class Solution {
    private List<int>[] g;
    private int[] informTime;

    public int NumOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        g = new List<int>[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new List<int>();
        }
        this.informTime = informTime;
        for (int i = 0; i < n; ++i) {
            if (manager[i] != -1) {
                g[manager[i]].Add(i);
            }
        }
        return dfs(headID);
    }

    private int dfs(int i) {
        int ans = 0;
        foreach (int j in g[i]) {
            ans = Math.Max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    }
}