README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/1300-1399/1376.Time%20Needed%20to%20Inform%20All%20Employees/README_EN.md	1561	Weekly Contest 179 Q3	Tree Depth-First Search Breadth-First Search

1376. Time Needed to Inform All Employees

中文文档

Description

A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company is the one with headID.

Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also, it is guaranteed that the subordination relationships have a tree structure.

The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.

The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e., After informTime[i] minutes, all his direct subordinates can start spreading the news).

Return the number of minutes needed to inform all the employees about the urgent news.

 

Example 1:

Input: n = 1, headID = 0, manager = [-1], informTime = [0]
Output: 0
Explanation: The head of the company is the only employee in the company.

Example 2:

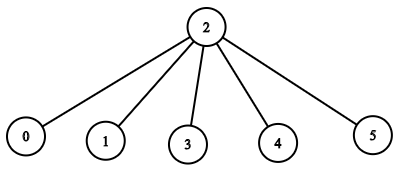
Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
Output: 1
Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.

 

Constraints:

• 1 <= n <= 105
• 0 <= headID < n
• manager.length == n
• 0 <= manager[i] < n
• manager[headID] == -1
• informTime.length == n
• 0 <= informTime[i] <= 1000
• informTime[i] == 0 if employee i has no subordinates.
• It is guaranteed that all the employees can be informed.

Solutions

Solution 1: DFS

We first build an adjacent list $g$ according to the $manager$ array, where $g[i]$ represents all direct subordinates of employee $i$.

Next, we design a function $dfs(i)$, which means the time required for employee $i$ to notify all his subordinates (including direct subordinates and indirect subordinates), and then the answer is $dfs(headID)$.

In function $dfs(i)$, we need to traverse all direct subordinates $j$ of $i$. For each subordinate, employee $i$ needs to notify him, which takes $informTime[i]$ time, and his subordinates need to notify their subordinates, which takes $dfs(j)$ time. We take the maximum value of $informTime[i] + dfs(j)$ as the return value of function $dfs(i)$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of employees.

Python3

class Solution:
    def numOfMinutes(
        self, n: int, headID: int, manager: List[int], informTime: List[int]
    ) -> int:
        def dfs(i: int) -> int:
            ans = 0
            for j in g[i]:
                ans = max(ans, dfs(j) + informTime[i])
            return ans

        g = defaultdict(list)
        for i, x in enumerate(manager):
            g[x].append(i)
        return dfs(headID)

Java

class Solution {
    private List<Integer>[] g;
    private int[] informTime;

    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        this.informTime = informTime;
        for (int i = 0; i < n; ++i) {
            if (manager[i] >= 0) {
                g[manager[i]].add(i);
            }
        }
        return dfs(headID);
    }

    private int dfs(int i) {
        int ans = 0;
        for (int j : g[i]) {
            ans = Math.max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        vector<vector<int>> g(n);
        for (int i = 0; i < n; ++i) {
            if (manager[i] >= 0) {
                g[manager[i]].push_back(i);
            }
        }
        function<int(int)> dfs = [&](int i) -> int {
            int ans = 0;
            for (int j : g[i]) {
                ans = max(ans, dfs(j) + informTime[i]);
            }
            return ans;
        };
        return dfs(headID);
    }
};

Go

func numOfMinutes(n int, headID int, manager []int, informTime []int) int {
	g := make([][]int, n)
	for i, x := range manager {
		if x != -1 {
			g[x] = append(g[x], i)
		}
	}
	var dfs func(int) int
	dfs = func(i int) (ans int) {
		for _, j := range g[i] {
			ans = max(ans, dfs(j)+informTime[i])
		}
		return
	}
	return dfs(headID)
}

TypeScript

function numOfMinutes(n: number, headID: number, manager: number[], informTime: number[]): number {
    const g: number[][] = new Array(n).fill(0).map(() => []);
    for (let i = 0; i < n; ++i) {
        if (manager[i] !== -1) {
            g[manager[i]].push(i);
        }
    }
    const dfs = (i: number): number => {
        let ans = 0;
        for (const j of g[i]) {
            ans = Math.max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    };
    return dfs(headID);
}

C#

public class Solution {
    private List<int>[] g;
    private int[] informTime;

    public int NumOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        g = new List<int>[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new List<int>();
        }
        this.informTime = informTime;
        for (int i = 0; i < n; ++i) {
            if (manager[i] != -1) {
                g[manager[i]].Add(i);
            }
        }
        return dfs(headID);
    }

    private int dfs(int i) {
        int ans = 0;
        foreach (int j in g[i]) {
            ans = Math.Max(ans, dfs(j) + informTime[i]);
        }
        return ans;
    }
}