東京ではエスカレータの右側は歩く人に空けるというのが暗黙のルールになっている。しかしエスカレータで歩くことについて問題視されることが増えてきている。その理由としては安全性と効率性の観点から指摘されている。安全性の観点からは、日本エレベーター協会が注意しているように[5]、歩行によってすれ違う際に衝突し事故の原因になったり、左手をなんらかの理由で使えない利用者が手すりに掴まれないなどの問題がある。実際、エスカレータでの事故数は増加傾向にある[6]。効率性の観点からは、状況によっては片側が歩行専用レーンであることによってニ列とも停止専用レーンである場合に比べて輸送効率が低くなることがあるとされている。直感的には停まっているよりも歩いた方が輸送効率が高くなりそうに思える。これは1人の利用者の移動にかかる時間という観点からは正しいが、利用者全体を考えたときに時間あたりの輸送人数という観点からは必ずしも正しくないとされている。実際、ロンドンの地下鉄で三週間に渡りエスカレータでの歩行の禁止を呼びかける実験を行ったところ、輸送効率は約30%増加した[4]。この理由として、歩行利用者が停止利用者に比べて稀である場合は、歩行レーンの空間が無駄になること、エスカレータの歩行利用者は停止利用者よりも前の人との間隔をあける傾向にあることなどが考えられる。実験が行われたロンドンの地下鉄のエスカレータは高さ23mと非常に長く、ほとんどの利用者は歩行しようとしていなかった[4]。
ここでは、上記以外の輸送効率に寄与する要因として、エスカレータに乗るまでの利用者の群集運動に注目する。エスカレータの手前に自発的に綺麗な列が形成されることもあるが、必ずしもそうはならない。エスカレータ乗り場の混雑により、利用者が乗り口に到達するまでの時間を長くしているという仮説のもと、シミュレーションによりその現象を確認し、その性質を調べることを目的とする。
[1]を参考に、セルオートマトンのフロアフィールドモデルによるエスカレータ乗り口への群集運動を実装した。 20x20マスの乗り場から、長さ10マスのエスカレータが上に伸びている状況を考えた。エスカレータには停止専用レーン・歩行専用レーンの二種類があり、対応して各エージェントは、停止専用レーンのみ利用するエージェント(stander)と歩行専用レーンのみ利用するエージェント(walker)のいずれかである。standerは停止専用レーンの入り口に向かって移動し、walkerは歩行専用レーンの入り口に向かって移動する。各エージェントのある時刻での移動は、各マスにおける目的地までの距離を表したフロアフィールドを用いて定められる。目的地の違いにより、standerとwalkerは異なるフロアフィールドを持ち、目的地とのマンハッタン距離により値を定めた。[1]より、緊急でない場合の群集運動はユークリッド距離よりもマンハッタン距離がふさわしい。目的地が複数ある場合はそれらへのマンハッタン距離の最小値を採用した。例えば、停止専用レーンが複数ある場合、standerは最も近い停止専用レーンを目的地として移動する。時刻tである位置(x,y)にいたエージェントaは時刻t+1で確率的にノイマン近傍[(x-1,y),(x+1,y),(x,y-1),(x,y+1)]のいずれかへ移動するか、その場に留まる。これは以下のルールで定められる。
- 目的地に到達しているエージェントはエスカレータに乗るため、乗り場から除外される。
- 到達していない場合、ノイマン近傍の中で時刻tにおいてエージェント(standerとwalker両方)がいない空いているセルを探す
- 空いているセルがない場合、その場に留まる
- 空いているセルがある場合、エージェントaのフロアフィールドの値を参照し、exp(-beta * d)に比例した確率で一つのセルを選択し、移動候補とする。ここでdはセルのフロアフィールドの値、betaは最短経路をどれだけ辿りたいかを表す正のパラメータで、値が大きいほど目的地に近いセルをほぼ確実に選ぶようになる。今回は10とした。
- すべてのエージェントの移動候補を計算したら、移動先が一致してしまっているペアがないかを確認する
- 他と移動先が一致しない移動候補は採用されて、対応するエージェントは時刻t+1で移動する
- 移動先が一致する移動候補がM個ある場合、確率μでそれらすべての移動候補が棄却され、対応するエージェントは移動しない。確率(1-μ)/MでMこの中から一つの移動候補が採用され、対応するエージェントのみ移動する。ここで、摩擦パラメータμは0から大きくするとエージェントは動けなくなりやすくなる。
以上の設定のもとで、n人のstanderとm人のwalkerが時刻0で乗り場にランダムに出現したあとで、すべてのエージェントがエスカレータに乗るまでの時間を測定する。これは、駅のホームに設置されたエスカレータで、一本の電車が到着した後、電車から降りたすべての客がホームからいなくなるまでの時間を想定したものである。 別の設定として、エージェントを一定の割合で発生させ続け、時間あたりのエージェント輸送量を求めることも考えられる。この場合はエスカレータに乗ってから降りるまでの移動も重要になる。しかし、今回は乗るまでの群集運動に注目するため、エスカレータに乗った後の移動はほぼ無視した。ただしシミュレーションを可視化した際に分かりやすいように、エスカレータに乗ったあとはstanderが1マスずつ、walkerは2マスずつ移動させた。([2]によれば、エスカレータ速度は0.5m.sで、エスカレータからみた歩行速度はおよそ0.5m/sであることから、歩行利用者は停止利用者にくらべて二倍の速度で移動する。)
シミュレーター本体はPythonでsimulator.pyに実装されている。AgentMapクラスはある時刻でのエージェントの存在分布を管理するためのもので、そのインスタンスに対してエージェント分布の初期化・移動ルールに必要な計算などを行える。Simulationクラスはシミュレーションの実行を管理する。インスタンス変数historyは各時刻のAgentMapのインスタンスのリストで、メソッドstepを実行するごとに次の時刻のAgentMapのインスタンスが新たに追加される。stepメソッドの中で移動候補の列挙や確率的な選択などの移動ルールが実行される。run_all_passメソッドによりすべてのエージェントがいなくなるまでstepメソッドを繰り返し実行する。その結果はanimateメソッドにより可視化され、gifアニメーションとして保存できる。
実験はPython3.7.3で行い、実行に必要なpythonライブラリはバージョンと共にrequirements.txtにまとめた。また、matplotlibでgifアニメーションを出力するためにはimagemagickのインストールが必要である。
エスカレータとしては停止専用レーンが隣接して2つあるとき(both stand)、停止専用レーンが1つで歩行専用レーンも隣接して1つあるとき(one stand)を考え、例としてone standで(n,m)=(90,10)の場合をμ=0でシミュレーションした結果は以下のようなgifアニメーションになる(animation_one_stand_s90w10.gif)。ここで、standerは青丸、walkerは赤丸で示されている。左はstanderのフロアフィールド、中央はwalkerのフロアフィールドをグラデーションで示しており、右はエスカレータの位置だけを示している。この結果はsimulation.pyを実行することで得られる。

さらに、standerとwalkerの人数によってすべてのエージェントがエスカレータに乗るまでの時間がどう変化するのかを調べるため、(n,m)=(5i, 100-5i), i=1,2,...,10として合計100人のエージェントが乗り場からいなくなるまでの時間を求めた。シミュレーションは確率的なため、それぞれの条件で10回シミュレーションし、以下の散布図を作成した。10回のシミュレーション結果の中央値を線で結んである。この結果はduration.pyを実行することで得られる。各シミュレーションにおいて、1000ステップ経ってもエージェントがエスカレータに乗らない場合は、その時点でシミュレーションを終了し後の解析で結果は使わないことにした。グラフの縦軸は正規化した完了時間で、100人のstanderに対し停止専用レーンが2つある時(both stand)の10回の完了時間の中央値を1としている。
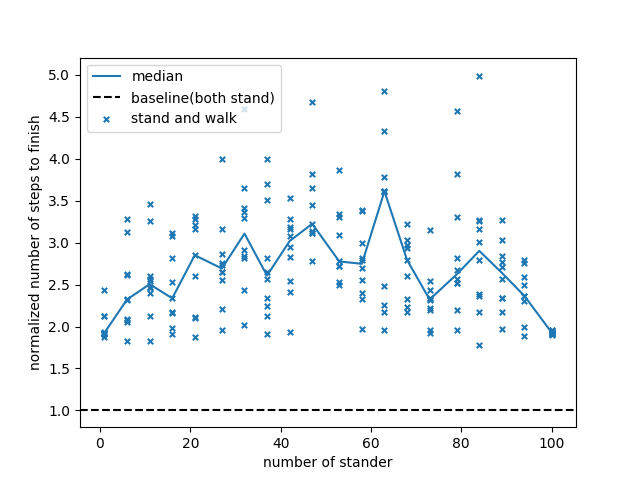
このグラフから、n=0や100付近で最小値、n=50付近で最大値をとることがわかる。これは、集団がほぼ均質であるときはスムーズに乗ることができるが、集団が多様になると相互作用により集団として搭乗に時間がかかるようになることを意味している。また、停止専用レーンを2つ用意した場合と比べて、最低でも2倍(均質集団のとき)、最大で3倍(多様集団のとき)の完了時間がかかることがわかる。
その他、μの大きさを0より大きくするとすべてのエージェントがいなくなるまでの時間が長くなることなどが観察されたが、明らかに直感的でない現象を見つけることはできなかった。
今回時間がなかったが、2つのエスカレータを離して設置した場合や、各エージェントが確率的にstanderとwalkerのタイプをスイッチする場合などは、興味のある状況である。
[1] 柳澤 大地, 西成 活裕. (2017) 人流シミュレーション:1.群集運動のセルオートマトンモデル. 情報処理 58 7 570 - 573. http://id.nii.ac.jp/1001/00182223/
[2] 元田 良孝,宇佐美誠史. エスカレーター内の歩行に関する基礎研究 http://p-www.iwate-pu.ac.jp/~motoda/JSTEmotoda18ver3.pdf
[3] 斗鬼 正一. エスカレーター片側空けという異文化と日本人のアイデンティティ. 江戸川大学紀要 (25), 35-50, 2015-03 http://id.nii.ac.jp/1193/00000538/
[4] The simulation that proves standing only escalators work on the Tube
[5] 一般社団法人 日本エレベーター協会|エスカレーターのご利用について
[6] 一般社団法人日本エレベーター協会. (2015). エスカレーターにおける利用者災害の調査報告(第8回)https://www.n-elekyo.or.jp/about/elevatorjournal/pdf/Journal7-13.pdf